\(B=\sqrt{x}-x=-\left(x-\sqrt{x}+\dfrac{1}{4}\right)+\dfrac{1}{4}=-\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{1}{4}\le\dfrac{1}{4}\)
\(B_{max}=\dfrac{1}{4}\) khi \(\sqrt{x}-\dfrac{1}{2}=0\Rightarrow x=\dfrac{1}{4}\)
Bt: Tìm GTLN của bt : \(B=-x^2+\sqrt{5}x-2\). GTLN đó đạt đc khi nào?
Cho bt:
\(Q=\dfrac{x+16}{\sqrt{x}+3}\)
Tìm GTLN của Q
Tìm GTLN, GTNN của bt: P = 3 căn(x) + 1
Cho Bt Q=\(\sqrt{\left(1-3x\right)\left(x+\frac{1}{2}\right)}\)
a) Với Gt nào của x thì bt Q có nghĩa ?
b) Tìm GTLN của Q khi Q có nghĩa
Cho Bt Q=\(\sqrt{\left(1-3x\right)\left(x+\frac{1}{2}\right)}\)
a) Với Gt nào của x thì bt Q có nghĩa ?
b) Tìm GTLN của Q khi Q có nghĩa
Cho Bt Q=\(\sqrt{\left(1-3x\right)\left(x+\frac{1}{2}\right)}\)
a) Với Gt nào của x thì bt Q có nghĩa ?
b) Tìm GTLN của Q khi Q có nghĩa
BT: Tìm gtln của bt: \(A=\sqrt{16-x^2}\)
Tìm x để bt đạt GTLN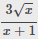 
Tìm GTLN của bt \(\frac{3\left(x+1\right)}{2-\sqrt{x}}\)
