b: \(-7x^2-4y^2-8xy+18x+9\)
\(=\left(-4x^2-8xy-4y^2\right)+\left(-3x^2+18x-27\right)+36\)
\(=-4\left(x^2+2xy+y^2\right)-3\left(x^2-6x+9\right)+36\)
\(=-4\left(x+y\right)^2-3\left(x-3\right)^2+36< =36\forall x,y\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x+y=0\\x-3=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=3\\y=-3\end{matrix}\right.\)
a.
Đặt \(A=-x^2-5y^2+4xy+12x+7\)
\(=-\dfrac{1}{5}\left(4x^2-20xy+25y^2\right)-\dfrac{1}{5}\left(x^2-60x+900\right)+187\)
\(=-\dfrac{1}{5}\left(2x-5y\right)^2-\dfrac{1}{5}\left(x-30\right)^2+187\le187\)
\(A_{max}=187\) khi \(\left(x;y\right)=\left(30;12\right)\)

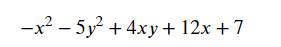
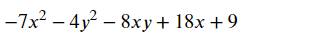 Tìm GTLN của biểu thức sau
Tìm GTLN của biểu thức sau












