Lời giải:
ĐKXĐ: $3\leq x\leq 5$
Áp dụng BĐT Bunhiacopkxy:
$(\sqrt{x-3}+\sqrt{5-x})^2\leq [(x-3)+(5-x)](1+1)=4$
$\Rightarrow \sqrt{x-3}+\sqrt{5-x}\leq 2$
Vậy $N_{\max}=2$. Giá trị này đạt tại $x=4$
Lời giải:
ĐKXĐ: $3\leq x\leq 5$
Áp dụng BĐT Bunhiacopkxy:
$(\sqrt{x-3}+\sqrt{5-x})^2\leq [(x-3)+(5-x)](1+1)=4$
$\Rightarrow \sqrt{x-3}+\sqrt{5-x}\leq 2$
Vậy $N_{\max}=2$. Giá trị này đạt tại $x=4$
Tìm giá trị lớn nhất ,giá trị nhỏ nhất của biểu thức
tìm giá trị lớn nhất , giá trị nhỏ nhất của biểu thức
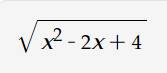
tìm giá trị lớn nhất , giá trị nhỏ nhất của biểu thức
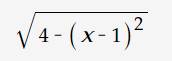
Tìm giá trị nhỏ nhất, giá trị lớn nhất của P = \(\dfrac{\sqrt{x}}{x+3\sqrt{x}+4}\)
:Tìm giá trị lớn nhất và giá trị nhỏ nhất của y=\(\dfrac{x^2+3}{x^2-x+2}\)
Cho biểu thức
M=căn x +1/2
A)Tìm các giá trị nguyên của x để M nhận giá trị nguyên
B)Tìm giá trị lớn nhất của biểu thức M
c)Tìm các giá trị nguyên của x để A nhận giá trị nguyên
Tìm giá trị lớn nhất của C = (3x + 4*(căn bậc hai của x) - 4) : x
Tìm giá trị lớn nhất của \(C=\frac{\left(3x+4\sqrt{x}-4\right)}{x}\)
tìm giá trị lớn nhất giá trị nhỏ nhất của biểu thức
y=-x2+40x+600
hứa tick 15 câu trả lời gần nhất cho ai trả lời
A= 2/căn3+3
tìm x để A đạt giá trị lớn nhất. tìm giá trị lớn nhất đó