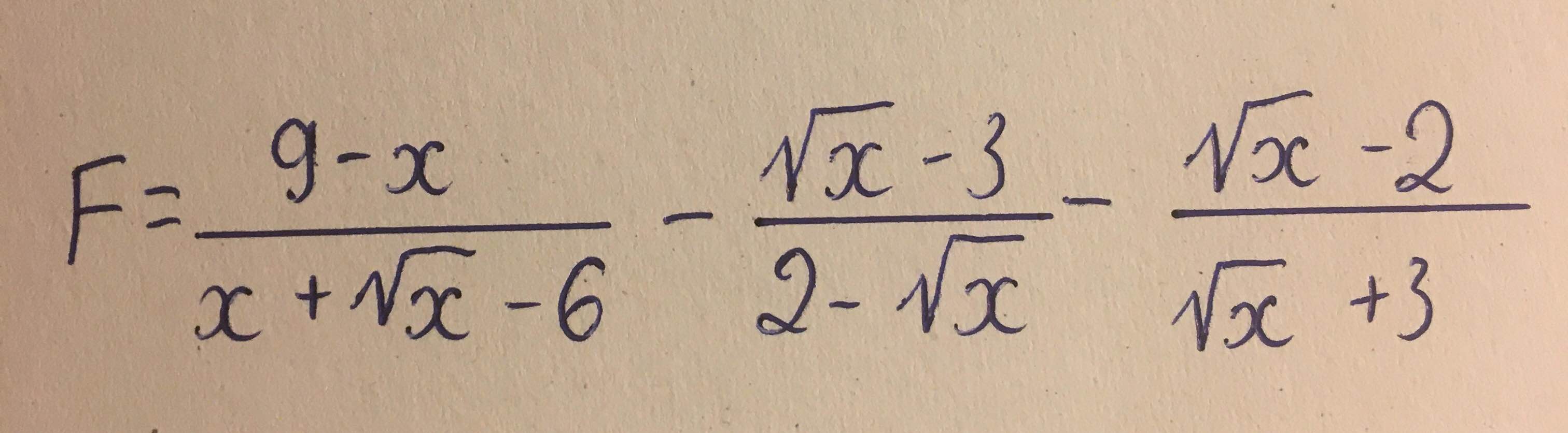\(F=\dfrac{9-x}{x+\sqrt{x}-6}-\dfrac{\sqrt{x}-3}{2-\sqrt{x}}-\dfrac{\sqrt{x}-2}{\sqrt{x}+3}\left(đk:x\ne4\right)=\dfrac{9-x+\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)-\left(\sqrt{x}-2\right)\left(\sqrt{x}-2\right)}{x+\sqrt{x}-6}=\dfrac{9-x+x-9-\left(\sqrt{x}-2\right)^2}{x+\sqrt{x}-6}=\dfrac{-\left(\sqrt{x}-2\right)^2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}=\dfrac{2-\sqrt{x}}{\sqrt{x}+3}\)
\(F=\dfrac{9-x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}+\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}-\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{9-x+x-9-\left(\sqrt{x}-2\right)^2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\) \(=\dfrac{-\left(\sqrt{x}-2\right)^2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}=\dfrac{1}{3-\sqrt{x}}\)
Ta có: \(F=\dfrac{9-x}{x+\sqrt{x}-6}-\dfrac{\sqrt{x}-3}{2-\sqrt{x}}-\dfrac{\sqrt{x}-2}{\sqrt{x}+3}\)
\(=\dfrac{9-x+x-9-x+4\sqrt{x}-4}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{-\left(\sqrt{x}-2\right)^2}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{2-\sqrt{x}}{\sqrt{x}+3}\)