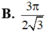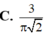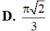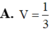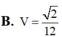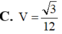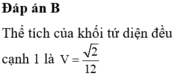Các câu hỏi tương tự
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích bằng 1. Trên cạnh SC lấy điểm E sao cho SE2EC. Tính thể tích V của khối tứ diện SEBD.
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích bằng 1. Trên cạnh SC lấy điểm E sao cho SE=2EC. Tính thể tích V của khối tứ diện SEBD.
![]()
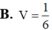
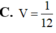
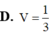
Cho khối chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh bằng 1, SA1 và SA
⊥
(ABC) . Tính thể tích của khối chóp đã cho.
Đọc tiếp
Cho khối chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh bằng 1, SA=1 và SA ⊥ (ABC) . Tính thể tích của khối chóp đã cho.
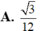
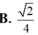
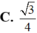
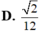
Cho hình chóp S.ABC có đáy là tam giác ABC đều cạnh 3a, cạnh bên SC2a và SC vuông góc với mặt phẳng đáy. Tính thể tích của khối cầu ngoại tiếp hình chóp S.ABC
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác ABC đều cạnh 3a, cạnh bên SC=2a và SC vuông góc với mặt phẳng đáy. Tính thể tích của khối cầu ngoại tiếp hình chóp S.ABC
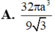
![]()
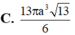
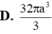
Một khối nón có diện tích đáy bằng 9p và diện tích xung quanh bằng 15p. Tính thể tích V của khối nón.
Đọc tiếp
Một khối nón có diện tích đáy bằng 9p và diện tích xung quanh bằng 15p. Tính thể tích V của khối nón.
![]()
![]()
![]()
![]()
Cho hình hộp đứng ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a và góc BAD
60
o
AB’ hợp với đáy (ABCD) một góc
30
o
Thể tích khối hộp là:
Đọc tiếp
Cho hình hộp đứng ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a và góc BAD= 60 o AB’ hợp với đáy (ABCD) một góc 30 o Thể tích khối hộp là:
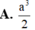
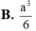
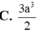
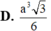
Cắt một khối trụ bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông có cạnh bằng 3a Tính diện tích toàn phần của khối trụ
Đọc tiếp
Cắt một khối trụ bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông có cạnh bằng 3a Tính diện tích toàn phần của khối trụ
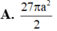
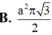
![]()
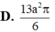
Cho khối cầu có thể tích là 36
π
(
c
m
3
). Bán kính R của khối cầu là
Đọc tiếp
Cho khối cầu có thể tích là 36 π ( c m 3 ). Bán kính R của khối cầu là
![]()
![]()
![]()
![]()
Cho lăng trụ đứng ABCD.ABCD có đáy là hı̀nh thoi cạnh 3a, góc
B
A
D
^
120
0
. Tı́nh thể tı́ch khối lăng trụ đã cho
A
.
2
3
a
3
B
.
27
3...
Đọc tiếp
Cho lăng trụ đứng ABCD.A'B'C'D' có đáy là hı̀nh thoi cạnh 3a, góc B A D ^ = 120 0 . Tı́nh thể tı́ch khối lăng trụ đã cho
A . 2 3 a 3
B . 27 3 a 3 2
C . 40 3 a 3
D . 3 a 3
Tỉ số thể tích giữa khối lập phương và khối cầu ngoại tiếp khối lập phương đó là
Đọc tiếp
Tỉ số thể tích giữa khối lập phương và khối cầu ngoại tiếp khối lập phương đó là