\(\Rightarrow C\\ \Leftrightarrow a^2=b^2+c^2-2b.c.cos\left(120\right)=b^2+c^2-2bc\dfrac{-1}{2}\\ =b^2+c^2+bc\)
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho tam giác ABC có A(1; -2; 3), B(0; 5; 6), C(1; 3; 2). Gọi H là hình chiếu vuông góc của A trên đường thẳng BC. Trong những khẳng định dưới đây, khẳng định nào sai? A. Một vectơ pháp tuyến của mặt phẳng (ABC) là: B. Một vectơ chỉ phương của đường thẳng AH là: C. AH ⊥ BC D. Các khẳng định trên không đồng thời đúng
Đọc tiếp
Cho tam giác ABC có A(1; -2; 3), B(0; 5; 6), C(1; 3; 2). Gọi H là hình chiếu vuông góc của A trên đường thẳng BC. Trong những khẳng định dưới đây, khẳng định nào sai?
A. Một vectơ pháp tuyến của mặt phẳng (ABC) là: ![]()
B. Một vectơ chỉ phương của đường thẳng AH là: ![]()
C. AH ⊥ BC
D. Các khẳng định trên không đồng thời đúng
Cho đường tròn (C) có phương trình
x
2
+
y
2
+
3
x
−
5
y
+
2
0
và ba điểm A(-1; 2), B(3; 0), C(2; 3). Khẳng định nào sau đây là đúng? A. Đường tròn (C) không cắt cạnh nào của tam giác ABC B.Đường tròn (C) chỉ cắt một cạnh của tam giác ABC C.Đường tròn (C) chỉ cắt hai cạnh của tam giác ABC...
Đọc tiếp
Cho đường tròn (C) có phương trình x 2 + y 2 + 3 x − 5 y + 2 = 0 và ba điểm A(-1; 2), B(3; 0), C(2; 3). Khẳng định nào sau đây là đúng?
A. Đường tròn (C) không cắt cạnh nào của tam giác ABC
B.Đường tròn (C) chỉ cắt một cạnh của tam giác ABC
C.Đường tròn (C) chỉ cắt hai cạnh của tam giác ABC
D.Đường tròn (C) cắt cả ba cạnh của tam giác ABC
Gọi S = \(m^2_a+m^2_b+m^2_c\) là tổng bình phương độ dài ba trung tuyến của tam giác ABC. Trong các mệnh đề sau mệnh đề nào đúng?
A. S = \(\dfrac{3}{4}\left(a^2+b^2+c^2\right)\)
B. S = \(a^2+b^2+c^2\)
D. S = 3\(\left(a^2+b^2+c^2\right)\)
C. S = \(\dfrac{3}{2}\left(a^2+b^2+c^2\right)\)
Cho tam giác ABC với A(1; 4), B(3; -2), C(4; 5) và đường thẳng ∆: 2x – 5y + 3 = 0. Khẳng định nào sau đây là đúng?
A. Đường thẳng ∆ không cắt cạnh nào của tam giác
B. Đường thẳng ∆ cắt 1 cạnh của tam giác
C. Đường thẳng ∆ cắt 2 cạnh của tam giác
D. Đường thẳng ∆ cắt 3 cạnh của tam giác
Cho tam giác ABC có A(1; 3; 5), B(-4; 0; -2), C(3; 9; 6). Gọi G là trọng tâm tam giác ABC. Trong những khẳng định dưới đây, khẳng định nào sai? A. Tọa độ của điểm G là (0;4;3) B. AG ⊥ BC C. Phương trình tham số của đường thẳng OG là: x 0, y 4t, z 3t D. Đường thẳng OG nằm trong hai mặt phẳng: (P): x 0, (Q): 3y - 4z 0
Đọc tiếp
Cho tam giác ABC có A(1; 3; 5), B(-4; 0; -2), C(3; 9; 6). Gọi G là trọng tâm tam giác ABC. Trong những khẳng định dưới đây, khẳng định nào sai?
A. Tọa độ của điểm G là (0;4;3)
B. AG ⊥ BC
C. Phương trình tham số của đường thẳng OG là: x = 0, y = 4t, z = 3t
D. Đường thẳng OG nằm trong hai mặt phẳng: (P): x = 0, (Q): 3y - 4z = 0
Cho tam giác ABC có diện tích là S. BC = a, AC = b, AB = c. G là trọng tâm tam giác. Chứng minh rằng:
a/ \(cotA=\dfrac{b^2+c^2-a^2}{4S}\)
b/ \(cotA+cotB+cotC=\dfrac{a^2+b^2+c^2}{4S}\)
c/ \(GA^2+GB^2+GC^2=\dfrac{1}{3}\left(a^2+b^2+c^2\right)\)
d/ \(b^2-c^2=a\left(b.cosC-c.cosB\right)\)
Cho tam giác ABC có ABC có A(2; 2; 1), B(4; 4; 2), C(-2; 4; -3). Vectơ nào dưới đây là vectơ chỉ phương của đường phân giác trong AD của tam giác ABC. A.
-
2
;
4
;
-
3
B.
6
;
0
;
5
C....
Đọc tiếp
Cho tam giác ABC có ABC có A(2; 2; 1), B(4; 4; 2), C(-2; 4; -3). Vectơ nào dưới đây là vectơ chỉ phương của đường phân giác trong AD của tam giác ABC.
A. - 2 ; 4 ; - 3
B. 6 ; 0 ; 5
C. 0 ; 1 ; - 1 3
D. - 4 3 ; - 1 3 ; - 1
Trong không gian Oxyz, cho ba điểm A(0; 0; 0), B(1; 2; 3), C(2; 3; 1). Gọi D là chân đường phân giác trong xuất phát từ đỉnh A của tam giác ABC. Trong các khẳng định dưới đây, khẳng định nào sai? A. AD ⊥ BC B. Một vectơ chỉ phương của đường thẳng AD là:
AB
→
+
AC
→
C. Một vectơ chỉ phương của đường thẳng AD là: D. Một vectơ chỉ phương của đường thẳng AD là: ...
Đọc tiếp
Trong không gian Oxyz, cho ba điểm A(0; 0; 0), B(1; 2; 3), C(2; 3; 1). Gọi D là chân đường phân giác trong xuất phát từ đỉnh A của tam giác ABC. Trong các khẳng định dưới đây, khẳng định nào sai?
A. AD ⊥ BC
B. Một vectơ chỉ phương của đường thẳng AD là: AB → + AC →
C. Một vectơ chỉ phương của đường thẳng AD là: 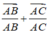
D. Một vectơ chỉ phương của đường thẳng AD là: u AD → = (1; 1; -2)
Cho tam giác ABC vuông cân tại A có
B
C
2
, M là trung điểm của BC. Khẳng định nào sau đây đúng A. B. C. D. Tất cả sai
Đọc tiếp
Cho tam giác ABC vuông cân tại A có B C = 2 , M là trung điểm của BC. Khẳng định nào sau đây đúng
A. ![]()
B. ![]()
C. ![]()
D. Tất cả sai





