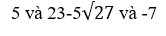Giả sử \(\sqrt[]{2}+\sqrt[]{3}< 3\)
\(\Leftrightarrow\left(\sqrt[]{2}+\sqrt[]{3}\right)^2< 3^2\)
\(\Leftrightarrow2+3+2\sqrt[]{6}< 9\)
\(\Leftrightarrow2\sqrt[]{6}< 4\)
\(\Leftrightarrow\left(2\sqrt[]{6}\right)^2< 4^2\)
\(\Leftrightarrow24< 16\left(sai\right)\)
Vậy \(\sqrt[]{2}+\sqrt[]{3}>3\)
Ta có :
\(\sqrt{2}+\sqrt{3}=\left(\sqrt{2}+\sqrt{3}\right)^2\\ =\left(\sqrt{2}\right)^2+2\cdot\sqrt{2}\cdot\sqrt{3}+\left(\sqrt{3}\right)^2\\ =2+2\sqrt{6}+3\\ =5+2\sqrt{6}\left(5+2\sqrt{6}>5+2\sqrt{4}\right)\)
Mà \(5+2\sqrt{4}=5+2\cdot2=5+4=9\)
\(\Rightarrow5+2\sqrt{6}>9\)
Nên \(\sqrt{2}+\sqrt{3}>3\)

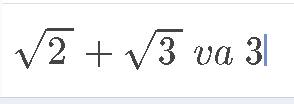 So sánh
So sánh






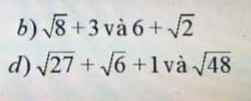
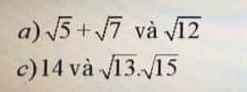
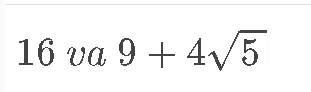 so sánh
so sánh