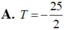\(y=f\left(x\right)=x^4-6mx+m^2\)
\(f'\left(x\right)=4x^3-12mx=4x\left(x^2-3m\right)\)
Xét \(m=0\Rightarrow\) thỏa
Xét \(m< 0\Rightarrow f\left(2\right)=m^2-24m+16>16\Rightarrow\) loại
Xét \(m>0\)
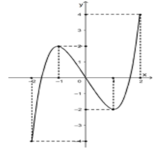
bbt:

\(TH_1:f\left(0\right)\) là giá trị lớn nhất của \(f\left(x\right)\) trên \(\left[-2,1\right]\)
\(\Rightarrow m^2=16\Rightarrow m=4\left(m>0\right)\)
Thử lại \(\Rightarrow\) thỏa
\(TH_2:f\left(-2\right)\) là giá trị lớn nhất của \(f\left(x\right)\) trên \(\left[-2,1\right]\) \(\)
\(\Rightarrow m^2-24m+16=16\Rightarrow m=24\)
Thử lại \(\Rightarrow\) loại
\(TH_3:f\left(1\right)\) là giá trị lớn nhất của \(f\left(x\right)\) trên \(\left[-2,1\right]\)
\(\Rightarrow m^2-6m+1=16\Rightarrow m=3+2\sqrt{6}\)
Thử lại \(\Rightarrow\) loại
Vậy chỉ có 2 giá trị m thỏa đề