Chọn D
Điều kiện: x ≠ m
Hàm số đã cho xác định trên [0;4] khi ![]()
Ta có 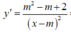
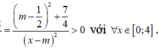
Hàm số đồng biến trên đoạn [0;4] nên 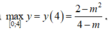
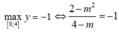
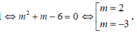
Kết hợp với điều kiện (*) ta được m = -3. Do đó có một giá trị của m thỏa yêu cầu bài toán.
Chọn D
Điều kiện: x ≠ m
Hàm số đã cho xác định trên [0;4] khi ![]()
Ta có 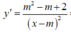
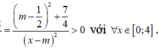
Hàm số đồng biến trên đoạn [0;4] nên 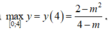
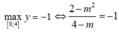
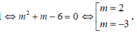
Kết hợp với điều kiện (*) ta được m = -3. Do đó có một giá trị của m thỏa yêu cầu bài toán.
Cho hàm số f(x) có đồ thị của hàm số f'(x) như hình vẽ. Biết f(0) + f(1) - 2f(2) = f(4) - f(3). Giá trị nhỏ nhất m, giá trị lớn nhất M của hàm số f(x) trên đoạn [0;4] là
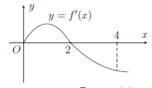
A. m = f(4), M = f(1)
B. m = f(4), M = f(2)
C. m = f(1), M = f(2)
D. m = f(0), M = f(2)
Có bao nhiêu giá trị thực của tham số m để giá trị lớn nhất của hàm số f ( x ) = x 2 - 2 x + m - 1 trên đoạn - 1 ; 2 bằng 6.
A. 1.
B. 4.
C. 3.
D. 2.
Tìm giá trị của tham số thực m để giá trị nhỏ nhất của hàm số y = 2 x + m x + 1 trên đoạn [0;4] bằng 3.
A. m = 3
B. m = 1
C. m = 7
D. m = 5
Cho hàm số y = m x + 1 2 x − 1 (m là tham số, m ≠ 2 ). Gọi a, b lần lượt giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên [1;3]. Khi đó có bao nhiêu giá trị của m để a . b = 1 5 .
A. 0
B. 2
C. 1
D. 3
Cho hàm số f(x) có đạo hàm là hàm f'(x). Đồ thị hàm số f'(x) như hình vẽ bên. Biết rằng f(0) + f(1) - 2f(2) = f(4) - f(3). Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của f(x) trên đoạn [0;4].

A. m = f(4), M = f(2)
B. m = f(1), M = f(2)
C. m = f(4), M = f(1)
D. m = f(0), M = f(2)
Có bao nhiêu giá trị nguyên dương của tham số m để giá trị nhỏ nhất của hàm số y = x + m 2 x - 1 trên đoạn [2;3] bằng 14.
A. 2
B. 1
C. 0
D. 4
Cho hàm số f(x) = x - m 2 + m x + 1 với m là tham số thực. Tìm tất cả các giá trị của m để hàm số có giá trị nhỏ nhất trên đoạn [0; 1] bằng – 2.
A. m= 1
B. m= -2
C. m= -1
D. m= -1 hoặc m= 2
Có tất cả bao nhiêu giá trị thực của tham số m để giá trị lớn nhất của hàm số y = x 2 - 2 x + m trên đoạn - 1 ; 2 bằng 5.
A. 3
B. 1
C. 2
D. 4
Giá trị lớn nhất M của hàm số y = x + 4 x + 1 trên đoạn [0;4]
A. M = 4
B. M = 24 5
C. M = 3
D. M = 6