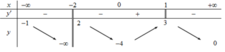
\(\lim\limits_{x\rightarrow-\infty}\dfrac{x-3}{\sqrt{x^2-9}}=-1\Rightarrow y=-1\) là 1 tiện cận ngang
\(\lim\limits_{x\rightarrow+\infty}\dfrac{x-3}{\sqrt{x^2-9}}=1\Rightarrow y=1\) là 1 TCN
\(\lim\limits_{x\rightarrow-3^-}\dfrac{x-3}{\sqrt{x^2-9}}=-\infty\) nên \(x=-3\) là 1 TCĐ
\(\lim\limits_{x\rightarrow3^+}\dfrac{x-3}{\sqrt{x^2-9}}=0\) và \(\lim\limits_{x\rightarrow3^+}\dfrac{x-3}{\sqrt{x^2-9}}\) ko tồn tại nên \(x=3\) ko phải tiệm cận
Vậy ĐTHS có 3 tiệm cận
Bn có thể tham khảo cách giải ở link này ạ:
https://tuhoc365.vn/qa/so-duong-tiem-can-cua-do-thi-ham-so-yx-3-can-x2-9-la/