a: sin x+cosx
=căn 2(sin x*1/căn 2+cosx*1/căn 2)
=căn 2*cos(x-pi/4)
b: sin x-cosx
=căn 2(sin x*1/căn 2-cosx *1/căn 2)
=căn 2*sin(x-pi/4)
Dựa vào các công thức cộng đã học:
sin(a + b) = sina cosb + sinb cosa;
sin(a – b) = sina cosb - sinb cosa;
cos(a + b) = cosa cosb – sina sinb;
cos(a – b) = cosa cosb + sina sinb;
và kết quả cos π/4 = sinπ/4 = √2/2, hãy chứng minh rằng:
a) sinx + cosx = √2 cos(x - π/4);
b) sin x – cosx = √2 sin(x - π/4).
Cho tam giác ABC có sinA+sinB= cosA+cosB. Chứng minh rằng tam giác ABC vuông.
Phương trình: c o s 4 x + sin 4 x + cos ( x - π 4 ) . sin ( 3 x - π 4 ) - 3 2 = 0 có nghiệm là:
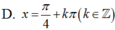
Xét tính chẵn lẻ của hàm số y = f(x) = cos(2x + π 4 ) + sin(2x - π 4 ), ta được
A. Hàm số chẵn.
B. Hàm số lẻ.
C. Không chẵn không lẻ.
D. Vừa chẵn vừa lẻ.
Tìm góc α ∈ π 6 ; π 4 ; π 3 ; π 2 để phương trình cos 2 x + 3 sin 2 x - 2 cos x = 0 tương đương với phương trình cos ( 2 x - α ) = cos x
Gọi α là nghiệm lớn nhất của phương trình 3.cos x + cos 2x – cos 3x + 1 = 2.sin x.sin 2x thuộc khoảng 0 , 2 π . Tính sin α - π 4 .
A . - 2 2
B . 2 2
C . 0
D . 1
CMR: Biểu thức sau không phụ thuộc vào x: A=-sin⁴x +cos⁴x + 2sin²x B=sin⁴x + cos²x × sin²x + cos²x C= cos⁴x + cos²x × sin²x + cos²x
Cho góc α cho thỏa 0 < α < π 4 và sin α + cos α = 5 2 Tính P = sin α -cos α .
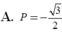
Giả sử A, B, C là ba góc của tam giác ABC, chứng minh rằng: sin A + sin B + sin C sin A + sin B - sin C = c o t A 2 c o t B 2
Giả sử A, B, C là ba góc của tam giác ABC, chứng minh rằng: sin A + sin B + sin C = 4 cos A 2 cos B 2 cos C 2
