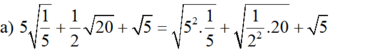
= √5 + √5 + √5 = 3√5
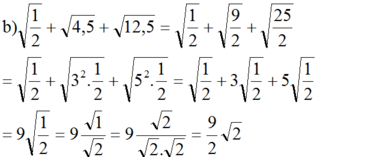
c) √20 - √45 + 3√18 + √72
= √4.5 - √9.5 + 3√9.2 + √36.2
= 2√5 - 3√5 + 9√2 + 6√2
= -√5 + 15√2
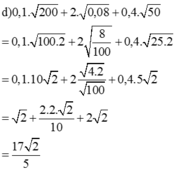
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
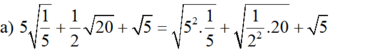
= √5 + √5 + √5 = 3√5
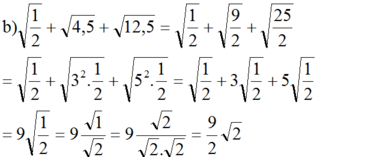
c) √20 - √45 + 3√18 + √72
= √4.5 - √9.5 + 3√9.2 + √36.2
= 2√5 - 3√5 + 9√2 + 6√2
= -√5 + 15√2
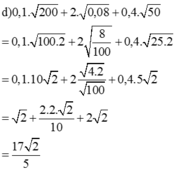
Rút gọn các biểu thức sau a)√27-✓12+✓48-5✓3 b)5✓18-✓5+✓20+✓1 2 C)✓25:✓16=✓36:✓9 D)✓12+✓27-5✓3 E)2✓3-✓75+2✓12
Câu 1
Rút gọn biểu thức A = √24 + 2√54 - 2√96
Câu 2
Rút gọn biểu thức A = 3√48 + √75 - 2√108
Câu 3
Rút gọn biểu thức A = √18 - 2√50 + 3√8
Câu 4
Tính giá trị biểu thức A = √18 + 2√8 - \(\dfrac{1}{5}\)√50
Câu 5
Rút gọn biểu thức M = √20 - √45 + √5
Câu 6
Tính giá trị biểu thức A = √5.(√5-3) + √45
Rút gọn biểu thức
a. 5√2x - 2√8 + 7√18 với x≥0
Giải phương trình
a.5√2x + 1 = 21
b. √4x + 20 - 3√5 + x + 7√9x + 45 = 20
Thực hiện phép tính (rút gọn biểu thức)
a)\(\sqrt{20}\)-3\(\sqrt{45}\)-\(\dfrac{1}{2}\sqrt{80}\)
b) 12\(\sqrt{54}\)-\(\dfrac{2}{5}\)\(\sqrt{150}\)+3\(\sqrt{24}\)
Rút gọn các biểu thức
\(B=\frac{9\sqrt{5}+3\sqrt{27}}{\sqrt{5}+\sqrt{3}} \)
\(C=\frac{\sqrt{2}+\sqrt{3}+\sqrt{6}+\sqrt{8}+4}{\sqrt{2}+\sqrt{3}+\sqrt{4}}\)
\(D=\frac{3\sqrt{8}-2\sqrt{12}+20}{3\sqrt{18}-2\sqrt{27}+\sqrt{45}}\)
rút gọn
a)3 √5 + √20-2 √5
b)2 √2+ √8+ √50
c) 4√3+ √ 27 -√45 +2 √5
d) √ 75+ √ 48- √300
e)( √28- √12- √7) √7 +2 √21
f)( √99- √18- √11) √11+3 √22
g)3 √45-5 √125x +7 √20x+28(x>=0)
b1,tính
a,\(\sqrt{\left(\sqrt{7}-4\right)^2}+\sqrt{8-2\sqrt{7}}\)
b,\(\sqrt{\left(\sqrt{5}-2\right)^2}+\sqrt{6+2\sqrt{5}}\)
b2,rút gọn các biểu thức sau
a,\(5\sqrt{\dfrac{1}{5}}+\dfrac{1}{2}\sqrt{20}+\sqrt{5}\)
b,\(\sqrt{\dfrac{1}{2}}+\sqrt{4,5}+\sqrt{12,5}\)
c,\(\sqrt{20}-\sqrt{45}+3\sqrt{18}+\sqrt{72}\)
d,\(0,1\times\sqrt{200}+2\times\sqrt{0,08}+0,4\times\sqrt{50}\)
Câu 1: Rút gọn các biểu thức sau:
A= (\(\sqrt{48}\) - 2\(\sqrt{3}\) + 2\(\sqrt{5}\) )\(\sqrt{5}\) - 2\(\sqrt{45}\)-\(\sqrt{3}\)
B= (\(\dfrac{1}{\sqrt{5}-\sqrt{2}}\)\(-\dfrac{1}{\sqrt{5}+\sqrt{2}}\)).\(\dfrac{1}{\left(\sqrt{2}+1\right)^2}\)
C= \(2\sqrt{a}\)-\(\sqrt{9a^3}\) a\(^2\) \(\sqrt{\dfrac{4}{a}}\)+ \(\dfrac{2}{a^2}\)\(\sqrt{25a^3}\) với a > 0
Rút gọn các biểu thức sau :
a) A= \(\sqrt{18}\) . \(\sqrt{2}\) - \(\sqrt{48}\) : \(\sqrt{3}\)
b)B= \(\dfrac{8}{\sqrt{5}-1}\) + \(\dfrac{8}{\sqrt{5}+1}\)
Bài 1 : Tính giá trị của biểu thức:
A = \(2\sqrt{5}-\sqrt{45} + 2\sqrt{20}\)
B = \((\sqrt{18} - 1/2.\sqrt{32}+ 12\sqrt{2}):\sqrt{2}\)
C = \((\sqrt{12} + 2\sqrt{27} - 3\sqrt{3})\sqrt{3}\)
D = \(\sqrt{20}-\sqrt{45}+3\sqrt{18}+\sqrt{72}\)
GIÚP MÌNH NHÉ. THANKS!