Các câu hỏi tương tự
Trong các khẳng định sau, khẳng định nào là sai?
A. \(\left(sinx+cosx\right)^2=1+2sinxcosx\)
B. \(sin^4x+cos^4x=1-2sin^2xcos^2x\)
C. \(\left(sinx-cosx\right)^2=1-2sinxcosx\)
D. \(sin^6x+cos^6x=1-sin^2xcos^2x\)
a) 1-cot^4xfrac{2}{sin^2x}-frac{1}{sin^4x}b)frac{1-2sinx.cosx}{cos^2-sin^2}frac{1-tanx}{1+tanx}c)frac{sin^2x}{sinx-cosx}+frac{sinx+cosx}{1-tanx}sinx+cosxd)sqrt{frac{1+cosx}{1-cosx}}-sqrt{frac{1-cosx}{1+cosx}}frac{2.cosx}{|sin|}e)tan^3x+tan^2x+tanx+1frac{sinx+cosx}{cos^3x}
Đọc tiếp
a) \(1-cot^4x=\frac{2}{sin^2x}-\frac{1}{sin^4x}\)
b)\(\frac{1-2sinx.cosx}{cos^2-sin^2}\)\(=\frac{1-tanx}{1+tanx}\)\(\)
c)\(\frac{sin^2x}{sinx-cosx}+\frac{sinx+cosx}{1-tanx}=sinx+cosx\)
d)\(\sqrt{\frac{1+cosx}{1-cosx}}-\sqrt{\frac{1-cosx}{1+cosx}}=\frac{2.cosx}{|sin|}\)
e)\(tan^3x+tan^2x+tanx+1=\frac{sinx+cosx}{cos^3x}\)
9 tháng 8 2023 lúc 21:09
Biết \(sinx+cosx=m\).
Tính giá trị biểu thức sau theo m: \(sin^3x+cos^3x\)
11 tháng 3 2022 lúc 9:59
\(\dfrac{sinx+cosx}{sinx}=\dfrac{sinx+cos^2\dfrac{x}{2}-sin^2\dfrac{x}{2}}{2cos\dfrac{x}{2}sin\dfrac{x}{2}}\)
\(0< x< 90\), chứng minh
CMR:
a, \(\frac{\cot^2x-\sin^2x}{\cot^2x-tan^2x}=sin^2x.\cos^2x\)
b, \(\frac{\tan x}{1-\tan^2x}.\frac{\cot^2-1}{\cot x}=1\)
c, \(\frac{1+\sin x.\cos x}{\sin^2x-\cos^2x}=\frac{\tan x+1}{\cot x+1}\)
d, \(\frac{\sin x+\cos x-1}{\sin x-cosx+1}=\frac{\cos x}{1+sinx}\)
Nếu sinx + cosx = 1/2 thì 3sinx + 2cosx bằng
Nếu sinx + cosx 1/2 thì 3sinx + 2cosx bằng
Đọc tiếp
Nếu sinx + cosx= 1/2 thì 3sinx + 2cosx bằng
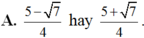
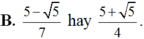
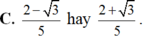
Rút gọn
A = \(\dfrac{sinx+sin2x+sin3x}{cosx+cos2x+cos3x}\)
Rút gọn P=cos6x-cos4x-sinx/sin6x+sin4x+cosx