\(R_N=\dfrac{R_1\cdot R_2}{R_1+R_2}=\dfrac{4\cdot12}{4+12}=3\Omega\)
\(I=\dfrac{\xi}{r+R_N}=\dfrac{6}{1+3}=1,5A\)
\(U_1=U_2=U=\xi-I\cdot r=6-1,5\cdot1=4,5V\)
\(I_1=\dfrac{U_1}{R_1}=\dfrac{4,5}{4}=1,125A\)
\(I_2=\dfrac{4,5}{12}=0,375A\)
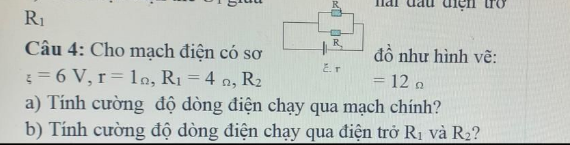
Tóm tắt:
\(\text{ξ }=6V\)
\(r=1\Omega\)
\(R_1=4\Omega\)
\(R_2=12\Omega\)
a. \(I=?\)
b. \(I_1=?;I_2=?\)
Giải:
a. Điện trở của mạch ngoài:
\(R_N=\dfrac{R_1R_2}{R_1+R_2}=\dfrac{4.12}{4+12}=3\Omega\)
Cường độ dòng điện qua mạch:
\(I=\dfrac{\text{ξ }}{R_N+r}=\dfrac{6}{3+1}=1,5A\)
b. Hiệu điện thế hai đầu mạch:
\(U_N=I.R_N=1,5.3=4,5V\)
Mà: \(R_1\text{/}\text{/}R_2\Rightarrow U_1=U_2=U_N=4,5V\)
Cường độ dòng điện qua điện trở \(R_1\) và \(R_2\)
\(I_1=\dfrac{U_1}{R_1}=\dfrac{4,5}{4}=1,125A\)
\(I_2=\dfrac{U_2}{R_2}=\dfrac{4,5}{12}=0,375A\)