1.
Không gian mẫu: \(C_{100}^3\)
Gọi 3 số được chọn là a;b;c
Theo t/c của cấp số cộng: \(a+c=2b\)
\(\Rightarrow a;c\) có cùng tính chẵn lẻ
Với mỗi cặp (a;c) luôn cho đúng 1 giá trị b tương ứng \(b=\dfrac{a+c}{2}\)
Tập S gồm 50 số chẵn và 50 số lẻ, nên số cặp (a;c) là: \(C_{50}^2+C_{50}^2\)
Xác suất: \(P=\dfrac{C_{50}^2+C_{50}^2}{C_{100}^3}=\dfrac{1}{66}\)
3.
Có 3 kiểu quà: sổ + cặp sách, sổ + bút, cặp sách + bút
Gọi x là số học sinh nhận quà sổ + cặp sách
y là số học sinh nhận sổ + bút
z là số học sinh nhận cặp sách + bút
\(\Rightarrow\left\{{}\begin{matrix}x+y+z=12\\x+y=7\\x+z=8\\y+z=9\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=3\\y=4\\z=5\\\end{matrix}\right.\)
Chọn 3 suất quà phát cho 3 em dạng x: \(C_{12}^3\) cách
Chọn 4 suất quà từ 12-3=9 suất còn lại phát cho 4 em dạng y: \(C_9^4\)
Còn 5 suất phát cho 5 em còn lại: \(C_5^5\)
\(\Rightarrow\)Không gian mẫu \(C_{12}^3.C_9^4.C_5^5\)
Số cách để Hòa và Bình nhận quà giống nhau:
TH1: Hòa Bình nhận kiểu 1 \(\Rightarrow\) 10 bạn còn lại có 5 bạn nhận kiểu 3, 4 bạn nhận kiểu 2, 1 bạn nhận kiểu 1
\(\Rightarrow C_{10}^5.C_5^4.C_1^1\) cách
TH2: Hòa Bình nhận kiểu 2 \(\Rightarrow\) 10 bạn còn lại có 3 bạn kiểu 1, 2 bạn kiểu 2, 5 bạn kiểu 3
\(\Rightarrow C_{10}^3.C_7^2.C_5^5\)
TH3: Hòa Bình nhận kiểu 3 \(\Rightarrow\) 10 bạn còn lại có 3 bạn kiểu 1, 4 bạn kiểu 2, 3 bạn kiểu 3
\(\Rightarrow C_{10}^3.C_7^4.C_3^3\)
Cộng 3 TH lại chia ko gian mẫu
2.
Không gian mẫu: \(12!\)
Kí hiệu N là nam, n là nữ. Có 2 kiểu xếp thỏa mãn
Kiểu 1:
NnNnNn
nNnNnN
Kiểu 2:
nNnNnN
NnNnNn
Nên số cách xếp thỏa mãn là: \(2.A_6^3.A_6^3.3!.3!\)
Xác suất: \(P=\dfrac{2.\left(A_6^3\right)^2.\left(3!\right)^2}{12!}=\dfrac{1}{462}\)
Mình diễn giải chi tiết theo thầy Lâm cho bạn dễ hiểu hơn.
Bài 1 :
Chọn ngẫu nhiên \(3\) số trong \(S\) có \(100\) số có : \(C_{100}^3\left(cách.chọn\right)\)
Chọn 2 số \(a;c\) có cùng tính chẵn lẻ :
- Cả 2 số đều chẵn: có \(C_{50}^2\left(cách.chọn\right)\)
- Cả 2 số đều lẻ : có \(C_{50}^2\left(cách.chọn\right)\)
Tổng số cách: \(C_{50}^2+C_{50}^2\left(cách.chọn\right)\)
Số còn lại: đượcược xác định duy nhất dựa vào công thức của cấp số cộng \(b=\dfrac{a+c}{2}\)\(\Rightarrow\) chỉ có \(1\) cách chọn
Áp dụng quy tắc nhân, tổng số cách chọn 3 số: \(\left(C_{50}^2+C_{50}^2\right).1=C_{50}^2+C_{50}^2\)
Xác suất \(P=\dfrac{C_{50}^2+C_{50}^2}{C_{100}^3}=\dfrac{1}{66}\)
Bài 2 :
- Mỗi học sinh có 12 cách chọn chỗ ngồi nên có \(12!\) cách sắp xếp \(12\) học sinh vào \(12\) ghế
- Chọn 6 học sinh nam và 6 học sinh nữ vào 1 bàn gồm 2 dãy ghế đối diện nhau mỗi dãy có 6 ghế có \(2\left(cách.chọn\right)\)
- Chọn 3 trong 6 bạn nam sắp xếp trong 1 dãy có \(A_6^3\left(cách.chọn\right)\)
- Chọn 3 trong 6 bạn nữ sắp xếp trong 1 dãy có \(A_6^3\left(cách.chọn\right)\)
- Trong 1 dãy chọn 3 bạn nam để đối diện và kế bên là nữ có \(3!\left(cách.chọn\right)\)
- Trong 1 dãy chọn 3 bạn nữ để đối diện và kế bên là nam có \(3!\left(cách.chọn\right)\)
Vậy số cách sắp xếp thỏa mãn đề bài là \(2.A_6^3.A_6^3.3!.3!\left(cách.chọn\right)\)
Xác suất \(P=\dfrac{2.A_6^3.A_6^3.3!.3!}{12!}=\dfrac{1}{462}\)

















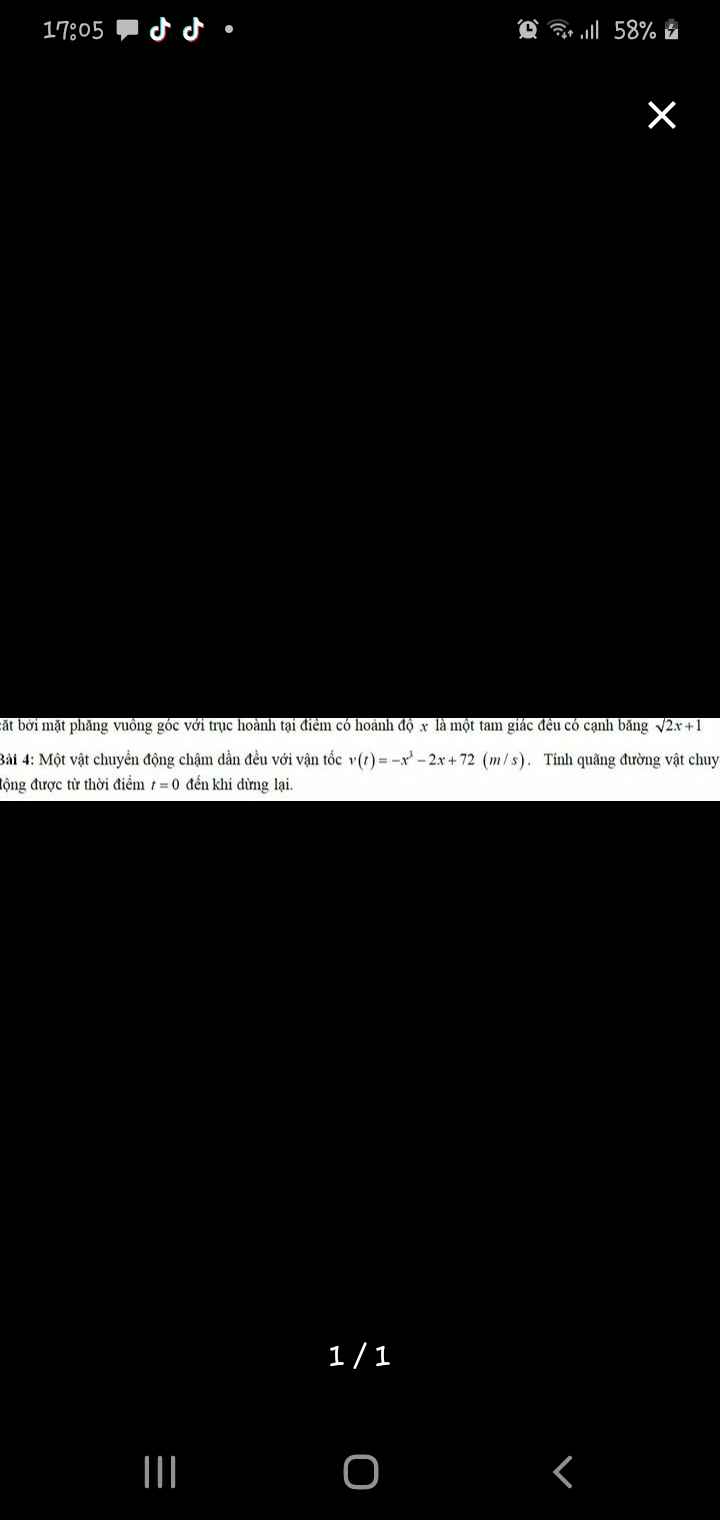 Em muốn hỏi là có thể gọi mấy cái x ở trong v (t) là ẩn t không ạ vì dạng này em thấy về ẩn t nên gặp cái ẩn x nó hơi hoang mang ạ nếu đc mn gthich cho em với ạ em cảm ơn 😢
Em muốn hỏi là có thể gọi mấy cái x ở trong v (t) là ẩn t không ạ vì dạng này em thấy về ẩn t nên gặp cái ẩn x nó hơi hoang mang ạ nếu đc mn gthich cho em với ạ em cảm ơn 😢