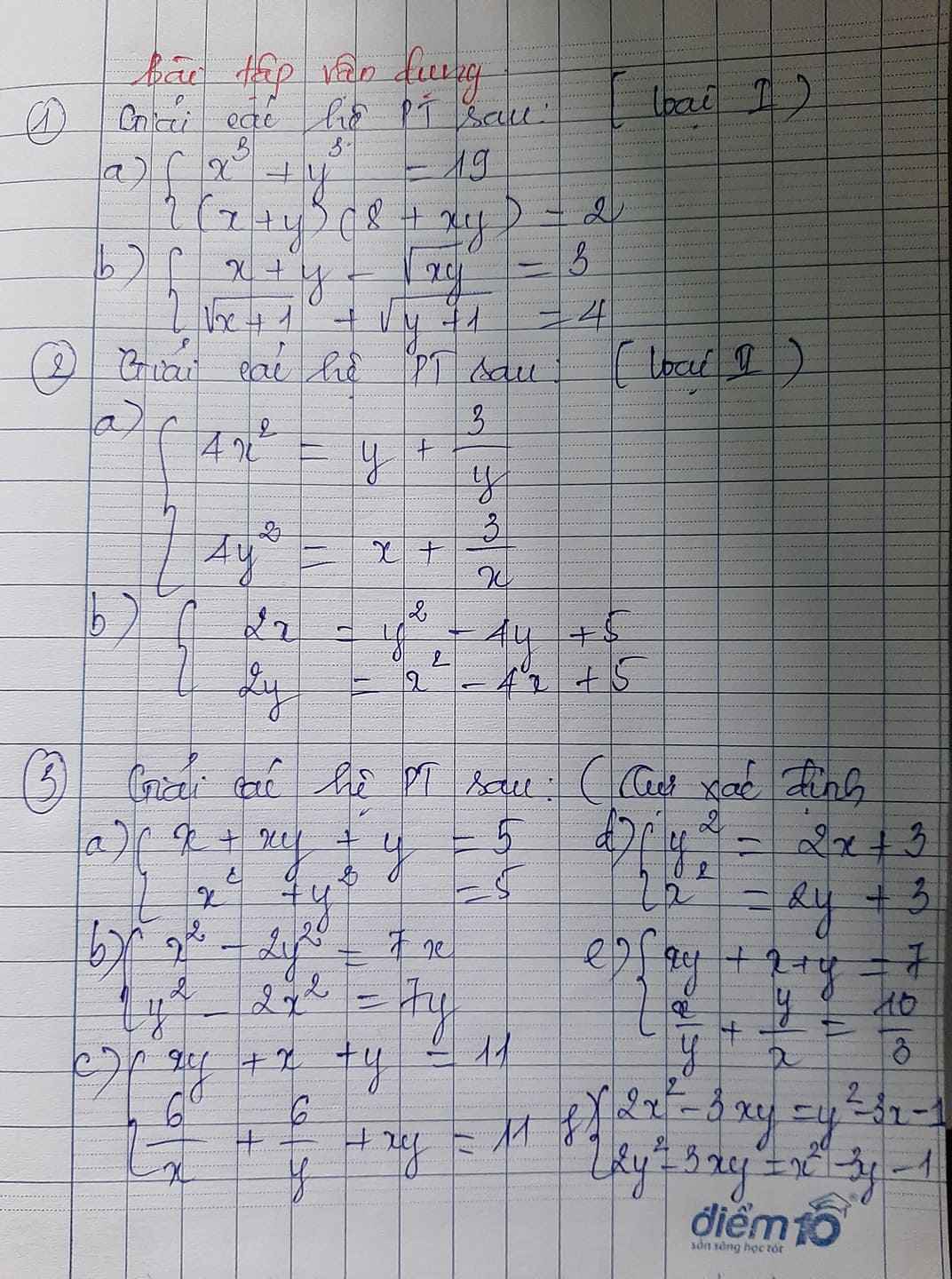Lời giải:
Theo định lý Viet:
$x_1+x_2=\frac{2}{2}=1$
$x_1x_2=\frac{-1}{2}$
Ta có:
$y_1+y_2=\frac{1}{x_1-1}+\frac{1}{x_2-1}=\frac{x_1+x_2-2}{(x_1-1)(x_2-1)}$
$=\frac{x_1+x_2-2}{x_1x_2-(x_1+x_2)+1}=\frac{1-2}{\frac{-1}{2}-1+1}=2$
$y_1y_2=\frac{1}{x_1-1}.\frac{1}{x_2-1}=\frac{1}{x_1x_2-(x_1+x_2)+1}$
$=\frac{1}{\frac{-1}{2}-1+1}=-2$
Theo định lý Viet đảo, $y_1,y_2$ là nghiệm của pt:
$y^2-2y-2=0$
Lời giải:
Theo định lý Viet:
$x_1+x_2=\frac{2}{2}=1$
$x_1x_2=\frac{-1}{2}$
Ta có:
$y_1+y_2=\frac{1}{x_1-1}+\frac{1}{x_2-1}=\frac{x_1+x_2-2}{(x_1-1)(x_2-1)}$
$=\frac{x_1+x_2-2}{x_1x_2-(x_1+x_2)+1}=\frac{1-2}{\frac{-1}{2}-1+1}=2$
$y_1y_2=\frac{1}{x_1-1}.\frac{1}{x_2-1}=\frac{1}{x_1x_2-(x_1+x_2)+1}$
$=\frac{1}{\frac{-1}{2}-1+1}=-2$
Theo định lý Viet đảo, $y_1,y_2$ là nghiệm của pt:
$y^2-2y-2=0$





 bài 3 câu c help pls
bài 3 câu c help pls