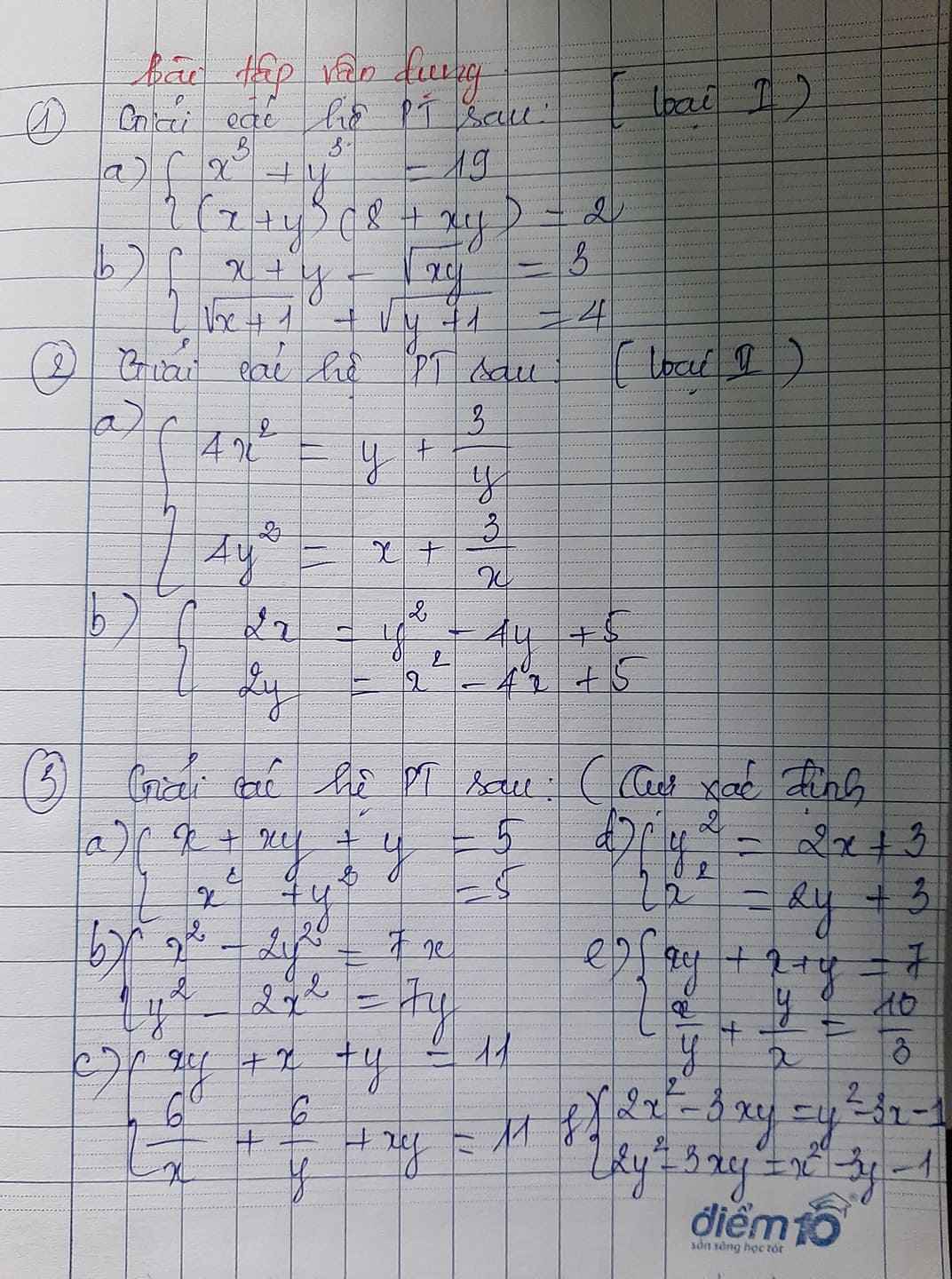2.
a)\(\left\{{}\begin{matrix}4x^2=y+\dfrac{3}{y}\\4y^2=x+\dfrac{3}{x}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4x^2:\dfrac{1}{y}=\left(y+\dfrac{3}{y}\right):\dfrac{1}{y}\\4y^2:\dfrac{1}{x}=\left(x+\dfrac{3}{x}\right):\dfrac{1}{x}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4x^2y=y^2+3\left(1\right)\\4y^2x=x^2+3\left(2\right)\end{matrix}\right.\) (1)-(2)<=>4x2y-4y2x=y2-x2
<=>4xy(x-y)=-(x-y)(x+y)<=>4xy(x-y)+(x-y)(x+y)=0
<=>(x-y)(x+y+4xy)=0<=>\(\left\{{}\begin{matrix}x-y=0=>x=y\\x+y+4xy=0=>x=\dfrac{-y}{1+4y}\end{matrix}\right.\)
Tới đó xét từng th rồi thế vô tìm x, y nha bạn.
b)\(\left\{{}\begin{matrix}2x=y^2-4y+5\left(1\right)\\2y=x^2-4x+5\left(2\right)\end{matrix}\right.\) (1)-(2)<=> 2x-2y=y2-x2-4y+4x
<=>(y-x)(y+x)+2(x-y)=0<=>(y-x)(y+x+2)=0
<=>\(\left\{{}\begin{matrix}x=y\\x=-2-y\end{matrix}\right.\)