\(64x^3-y^3\\ =\left(4x\right)^3-y^3\\ =\left(4x-y\right)\left[\left(4x\right)^2+4xy+y^2\right]\\ =\left(4x-y\right)\left(16x^2+4xy+y^2\right)\)
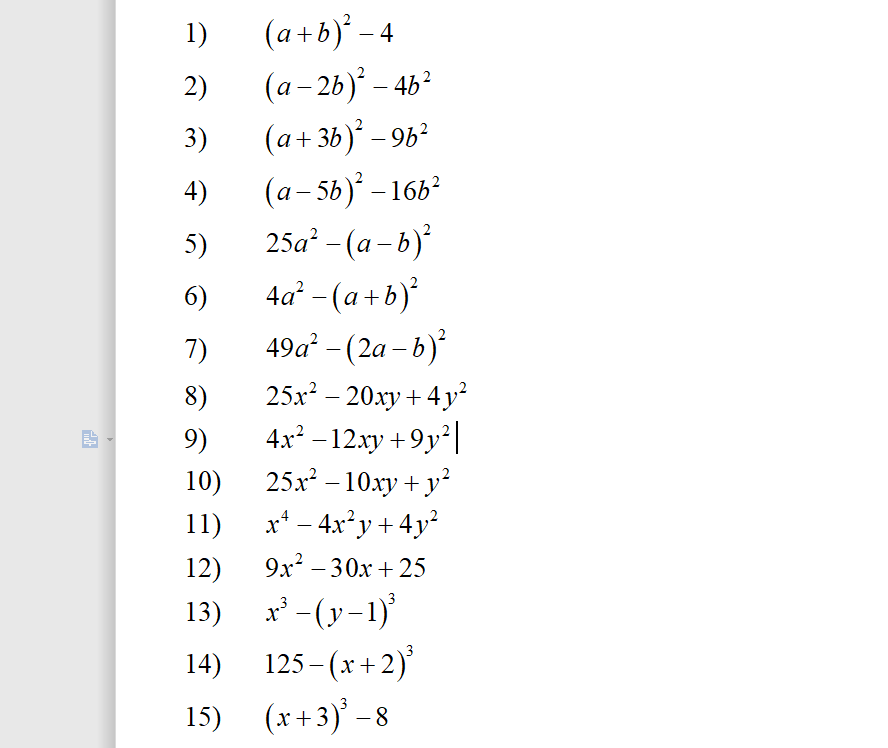
\(64x^3-y^3\)
\(=\left(4x\right)^3-y^3\)
\(=\left(4x-y\right)\left(16x^2+4xy+y^2\right)\)
Trong biểu thức bài toán cho, chúng ta cần lựa chọn ra những ẩn số hay hằng của một số biểu thức nhất định là ước chung và chọn chúng làm nhân tử. Để dễ hiểu chúng ta có như sau:
A.B + C.B - B.Q=B.(A + C-Q)
Mấu chốt của vấn đề là làm thế nào chúng ta phải đưa được biểu thức đã cho về dạng tích của nhiều đa thức. Bởi nhiều bạn mới học, cũng bảo đặt nhân tử chung nhưng khi xem kết quả thì chưa tồn tại dạng tích mà vẫn ở dạng tổng.
Ví dụ: Phân tích đa thức sau thành nhân tử bằng phương pháp đặt nhân tử chung.
64x3−y3=(4x)3−y3=(4x−y)[(4x)2+4xy+y2]=(4x−y)(16x2+4xy+y2)

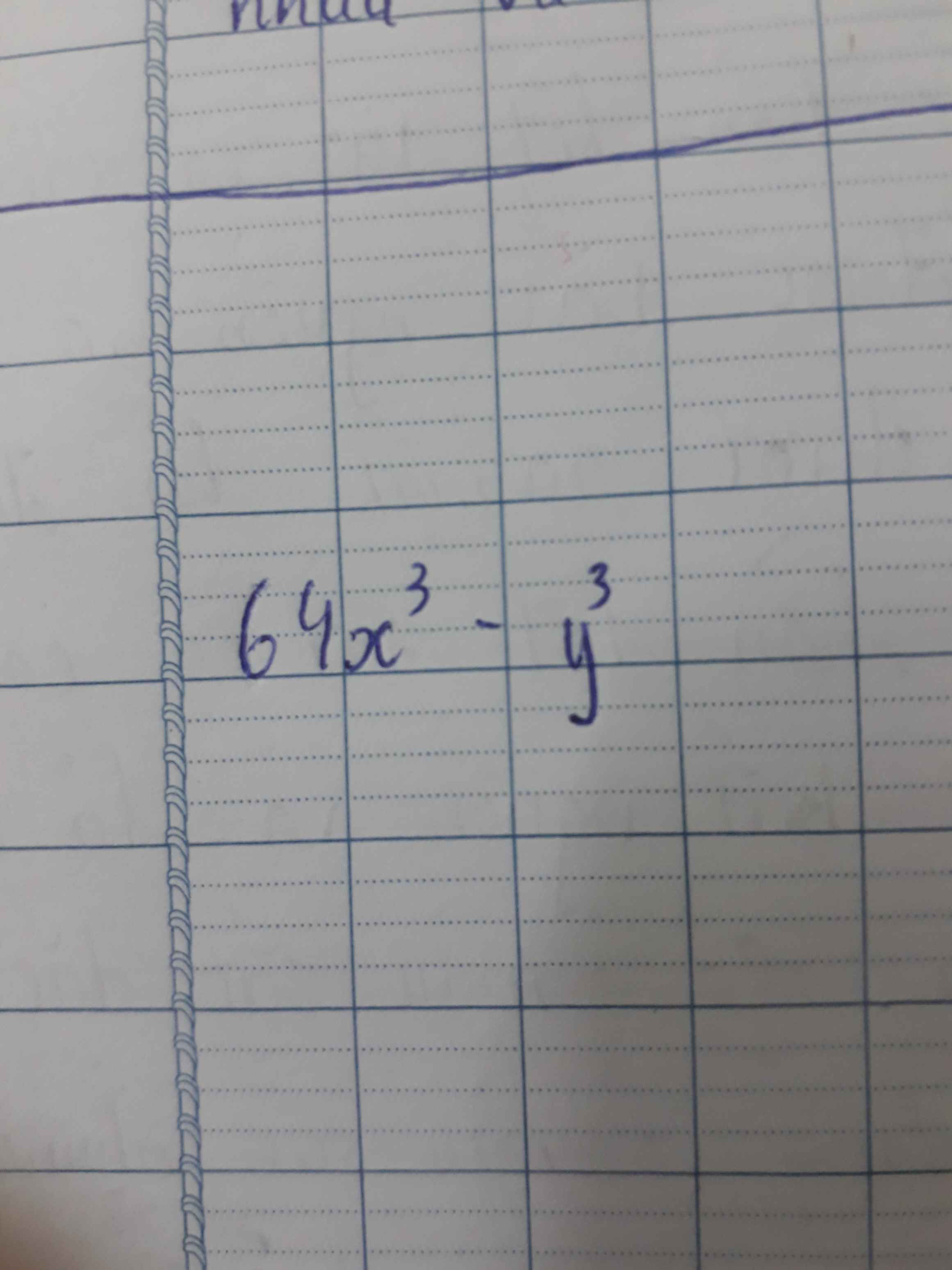

















 phân tích đa thức sau thành nhân tử(tách 1 hạng tử thành nhiều hangj tử(kè công thức dùm )
phân tích đa thức sau thành nhân tử(tách 1 hạng tử thành nhiều hangj tử(kè công thức dùm ) phân tích đa thức sau thành nhân tử(tách 1 hạng tử thành nhiều hạng tử)
phân tích đa thức sau thành nhân tử(tách 1 hạng tử thành nhiều hạng tử)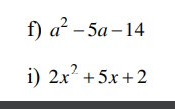 phân tích đa thức sau thành nhân tử(tách 1 hạng tử
phân tích đa thức sau thành nhân tử(tách 1 hạng tử