Phần Hình Học :
Bài 1 : Cho Δ ABC vuông tại A có AH là đường cao, đường trung tuyến AM. Qua H kẻ HD // AC ( D ∈ AC). Đoạn DP cắt AH, AM lần lượt tại O và N.
a, Chứng minh AH = DP.
b, ΔMAC là tam giác gì ?
c, Chứng minh ΔAPN là tam giác vuông.
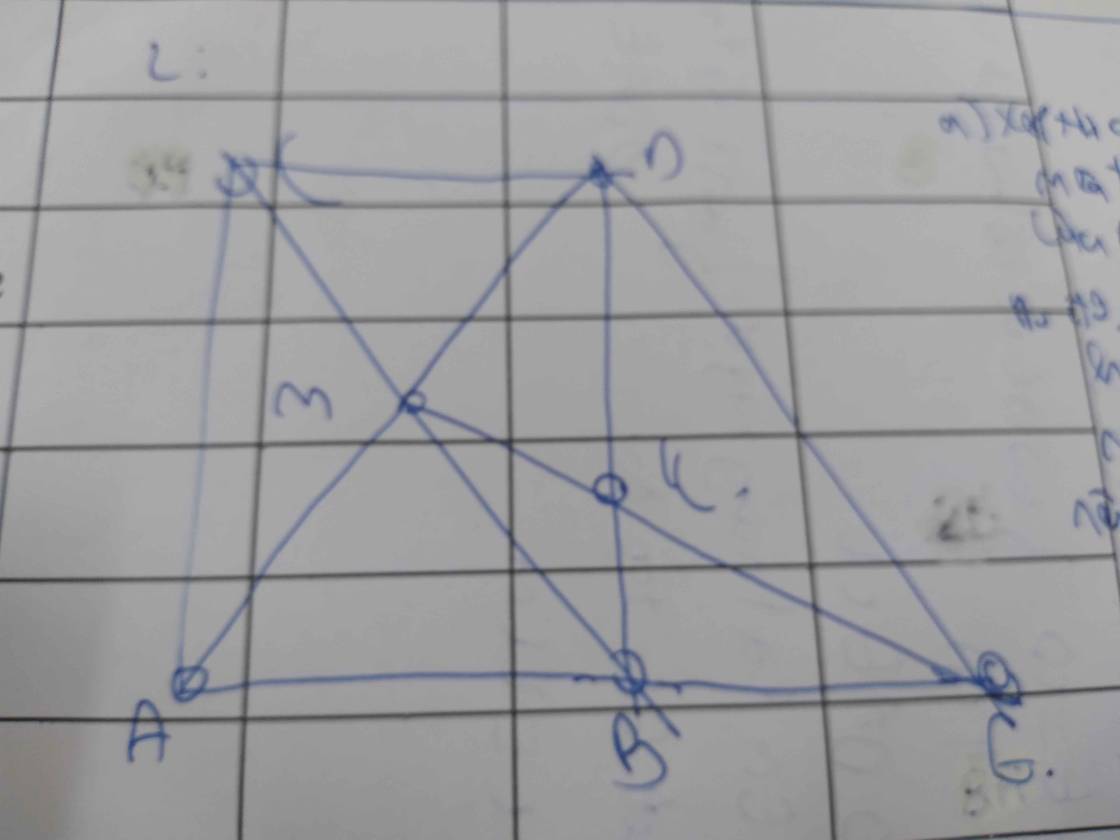
Bài 2. Cho ΔABC vuông tại A có AB < AC. Gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MD = MA.
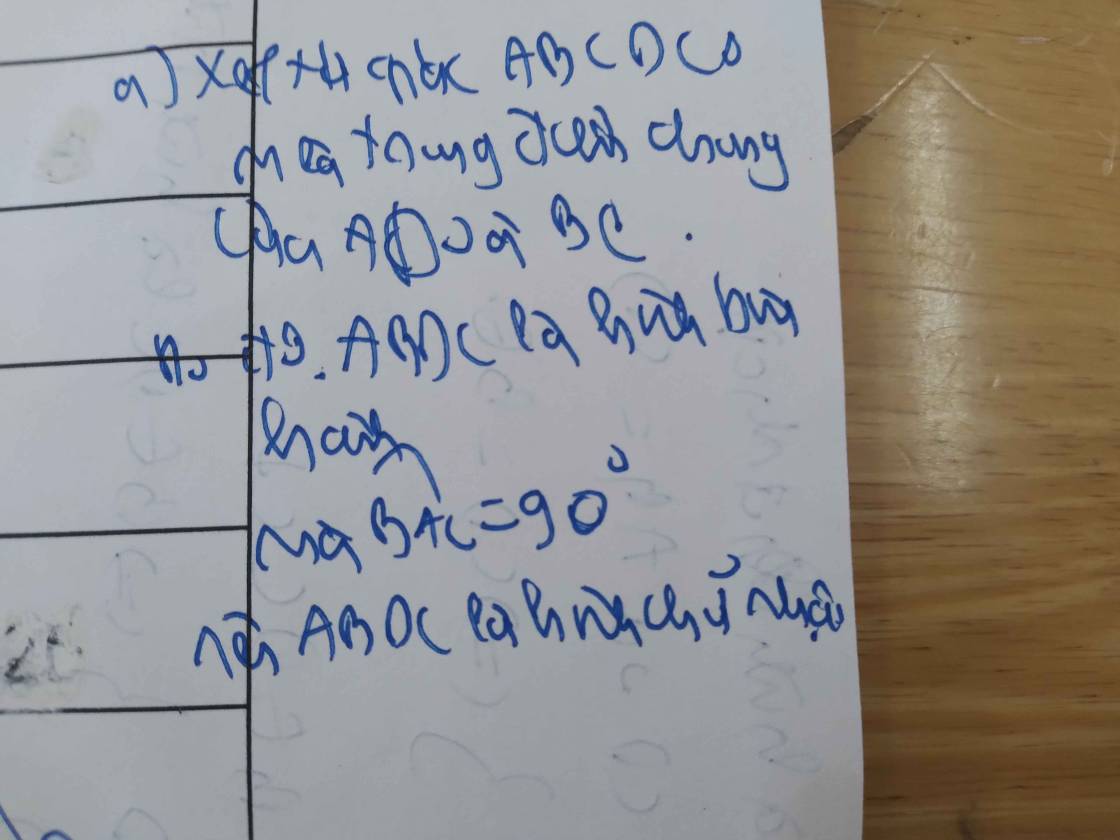
a, Chứng minh ABCD là hình chữ nhật.
b, Lấy điểm E sao cho B là trung điểm của AE. Chứng minh BEDC là hình bình hành.
c, EM cắt BD tại K. Chứng minh EK = 2KM.