Question

phần  d ạ

Answer 1

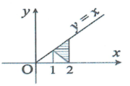
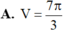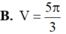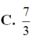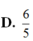Lời giải:
\(y_M< -4\Leftrightarrow \frac{-x_M^2+2x_M-5}{x_M-1}+4<0\\ \Leftrightarrow \frac{-x_M^2+6x_M-9}{x_M-1}<0\\ \Leftrightarrow \frac{-(x_M-3)^2}{x_M-1}<0\\ \Leftrightarrow \frac{(x_M-3)^2}{x_M-1}>0\) 

Do $x_M-1>0$ nên $(x_M-3)^2>0\Leftrightarrow x_M\neq 3$

Có:

\(IM^2=(x_M-1)^2+y_M^2=(x_M-1)^2+\frac{(x_M^2-2x_M+5)^2}{(x_M-1)^2}\\ =(x_M-1)^2+\frac{[(x_M-1)^2+4]^2}{(x_M-1)^2}\\ =a^2+\frac{(a^2+4)^2}{a^2}\)

Ta cần tìm $a>1, a\neq 2$ sao cho $IM^2 = a^2+\frac{(a^2+4)^2}{a^2}$ min.

Có:

$IM^2=a^2+\frac{(a^2+4)^2}{a^2}=2a^2+\frac{16}{a^2}+8$

$\geq 2\sqrt{2a^2.\frac{16}{a^2}}+8=8\sqrt{2}+2$
Dấu "=" xảy ra khi $2a^2=\frac{16}{a^2}, a>1$

$\Leftrightarrow a=\sqrt[4]{8}$

$\Leftrightarrow x_M=\sqrt[4]{8}-1$

$y_M=\frac{-x_M^2+2x_M-5}{x_M-1}=4-\frac{2\sqrt{2}}{\sqrt[4]{8}-2}$

Answer 2

18.

\(P'\left(t\right)=\dfrac{540.e^{-0,75t}}{\left(2+3.e^{-0,75t}\right)^2}\le4\)

Đặt \(e^{-0,75t}=x>0\)

\(\Rightarrow\dfrac{540x}{\left(2+3x\right)^2}\le4\)

\(\Rightarrow\left(3x+2\right)^2-135x\ge0\)

\(\Rightarrow9x^2-123x+4\ge0\Rightarrow\left[{}\begin{matrix}x\ge13,63\\x\le0,03\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}e^{-0,75t}\ge\dfrac{41+3\sqrt{185}}{6}\\e^{-0,75t}\le\dfrac{41-3\sqrt{185}}{6}\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}t\le\dfrac{ln\left(\dfrac{41+3\sqrt{185}}{6}\right)}{-,075}=-3,5\left(loại\right)\\t\ge\dfrac{ln\left(\dfrac{41-3\sqrt{185}}{6}\right)}{-0,75}\approx5\left(giờ\right)\end{matrix}\right.\)

Vậy \(t_{min}=5\) giờ

Answer 3

19.

Nếu \(a=0\Rightarrow f\left(x\right)\) là hàm bậc 2 nên luôn luôn ko đồng biến hoặc nghịch biến trên R (ktm)

\(\Rightarrow a\ne0\) 

hệ số bậc 3 của \(f\left(x\right)\) là a nên \(f\left(x\right)\) đồng biến trên R \(\Rightarrow a>0\)

\(\Rightarrow f\left(x\right)=0\) có 3 nghiệm: \(\left[{}\begin{matrix}x=-2a\\x=a-2b\\x=-\dfrac{1}{a}\end{matrix}\right.\) (1)

Mặt khác do \(f\left(x\right)\) đồng biến trên R nên \(f\left(x\right)=0\) có tối đa 1 nghiệm

\(\Rightarrow3\) nghiệm của (1) trùng nhau

\(\Rightarrow-2a=a-2b=-\dfrac{1}{a}\)

\(\Rightarrow\left\{{}\begin{matrix}-2a=-\dfrac{1}{a}\\-2a=a-2b\\\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a^2=\dfrac{1}{2}\\b=\dfrac{3a}{2}\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}a=\dfrac{1}{\sqrt{2}}\\b=\dfrac{3}{2\sqrt{2}}\end{matrix}\right.\)

Answer 4

20.

\(y'=3ax^2+2bx+c\)

Đồ thị tiếp xúc Ox tại P 

\(\Rightarrow\left\{{}\begin{matrix}y'\left(-2\right)=0\\y\left(-2\right)=0\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}12a-4b+c=0\\-8a+4b-2c+5=0\\\end{matrix}\right.\) (1)

Q là giao của y và Oy \(\Rightarrow x_Q=0\)

\(y'\left(x_Q\right)=3\Rightarrow y'\left(0\right)=3\)

\(\Rightarrow c=3\) (2)

(1);(2)  \(\Rightarrow\left\{{}\begin{matrix}12a-4b+c=0\\-8a+4b-2c=-5\\c=3\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}a=-\dfrac{1}{2}\\b=-\dfrac{3}{4}\\c=3\end{matrix}\right.\)