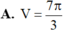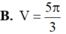Các câu hỏi tương tự
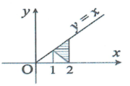
Cho hình phẳng H (phần gạch chéo trong hình vẽ). Thể tích khối tròn xoay tạo thành khi quay hình H quanh trục Ox được tính theo công thức nào dưới đây?
Đọc tiếp
Cho hình phẳng H (phần gạch chéo trong hình vẽ). Thể tích khối tròn xoay tạo thành khi quay hình H quanh trục Ox được tính theo công thức nào dưới đây?
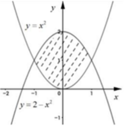
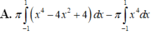
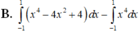

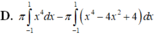
Cho hình vuông OABC có cạnh bằng 4 được chia thành hai phần bởi parabol (P) có đỉnh tại O. Gọi S là hình phẳng không bị gạch (như hình vẽ). Tính thể tích V của khối tròn xoay khi cho phần S quay quanh trục Ox. A. . B. . C. . D. .
Đọc tiếp
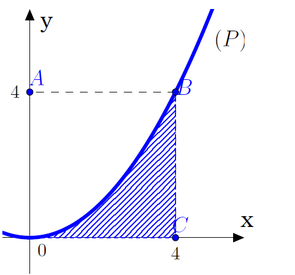
Cho hình vuông OABC có cạnh bằng 4 được chia thành hai phần bởi parabol (P) có đỉnh tại O. Gọi S là hình phẳng không bị gạch (như hình vẽ). Tính thể tích V của khối tròn xoay khi cho phần S quay quanh trục Ox.
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hình vuông OABC có cạnh bằng 4 được chia thành hai phần bởi parabol (P) có đỉnh tại O. Gọi S là hình phẳng không bị gạch (như hình vẽ). Tính thể tích V của khối tròn xoay khi cho phần S quay quanh trục Ox. A. B. C. D.
Đọc tiếp
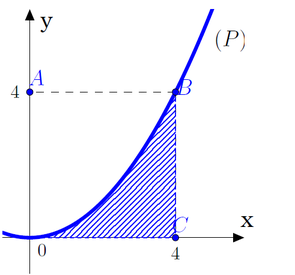
Cho hình vuông OABC có cạnh bằng 4 được chia thành hai phần bởi parabol (P) có đỉnh tại O. Gọi S là hình phẳng không bị gạch (như hình vẽ). Tính thể tích V của khối tròn xoay khi cho phần S quay quanh trục Ox.
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Cho hình vuông OABC có cạnh bằng 4 được chia thành hai phần bởi đường parabol (P) có đỉnh tại O. Gọi S là hình phẳng không bị gạch (như hình vẽ). Tính thể tích V của khối tròn xoay khi cho phần S quay quanh trục Ox
Đọc tiếp
Cho hình vuông OABC có cạnh bằng 4 được chia thành hai phần bởi đường parabol (P) có đỉnh tại O. Gọi S là hình phẳng không bị gạch (như hình vẽ). Tính thể tích V của khối tròn xoay khi cho phần S quay quanh trục Ox
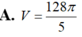
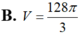
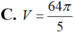
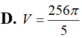
Cho hai đường tròn
O
1
;
5
và
O
2
;
3
cắt nhau tại hai điểm A, B sao cho AB là một đường kính của đường tròn
O
2
. Gọi (D) là hình phẳng được giới hạn bởi hai đường tròn (ở ngoài đường tròn lớn, phần gạch chéo...
Đọc tiếp
Cho hai đường tròn O 1 ; 5 và O 2 ; 3 cắt nhau tại hai điểm A, B sao cho AB là một đường kính của đường tròn O 2 . Gọi (D) là hình phẳng được giới hạn bởi hai đường tròn (ở ngoài đường tròn lớn, phần gạch chéo như hình vẽ). Quay (D) quanh trục O 1 O 2 ta được một khối tròn xoay. Tính thể tích V của khối tròn xoay được tạo thành
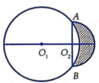
A. V = 14 π 3
B. V = 68 π 3
C. V = 40 π 3
D. V = 36 π
Cho (H) là hình phẳng giới hạn bởi
1
4
cung tròn có bán kính R2, đường cong
y
4
-
x
và trục hoành ( miền tô đậm như hình vẽ). Tính thể tích V của khối tạo thành khi cho hình (H) quay quanh trục Ox.
Đọc tiếp
Cho (H) là hình phẳng giới hạn bởi 1 4 cung tròn có bán kính R=2, đường cong y = 4 - x và trục hoành ( miền tô đậm như hình vẽ). Tính thể tích V của khối tạo thành khi cho hình (H) quay quanh trục Ox.
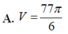
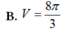
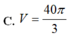
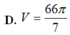
Cho hình phẳng (D) giới hạn bởi các đường y
x
-
2
2
và y 4. Tính thể tích của vật thể tròn xoay sinh ra bởi hình (D) khi nó quay xung quanh trục Ox A.
118
π
5
B.
253
π
7
C....
Đọc tiếp
Cho hình phẳng (D) giới hạn bởi các đường y= x - 2 2 và y = 4. Tính thể tích của vật thể tròn xoay sinh ra bởi hình (D) khi nó quay xung quanh trục Ox
A. 118 π 5
B. 253 π 7
C. 112 π 3
D. 256 π 5
Khi quay hình phẳng được đánh dấu ở hình vẽ bên xoay quanh trục Ox ta được một khối tròn xoay có thể tích được tính theo công thức A. B. C. D.
Đọc tiếp
Khi quay hình phẳng được đánh dấu ở hình vẽ bên xoay quanh trục Ox ta được một khối tròn xoay có thể tích được tính theo công thức
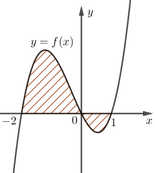
A. 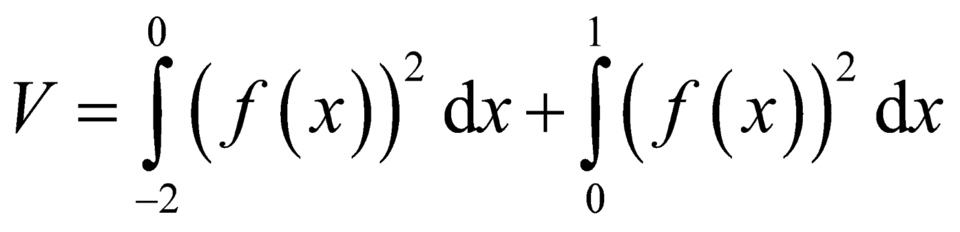
B. 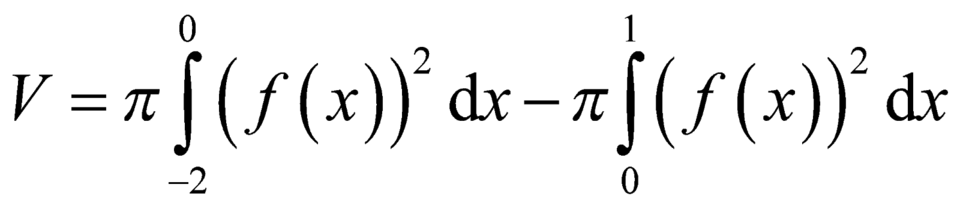
C. 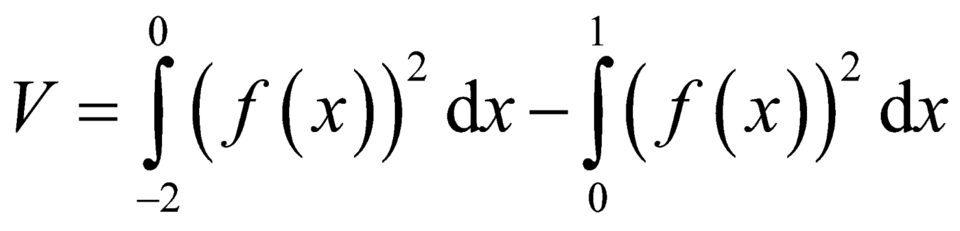
D. 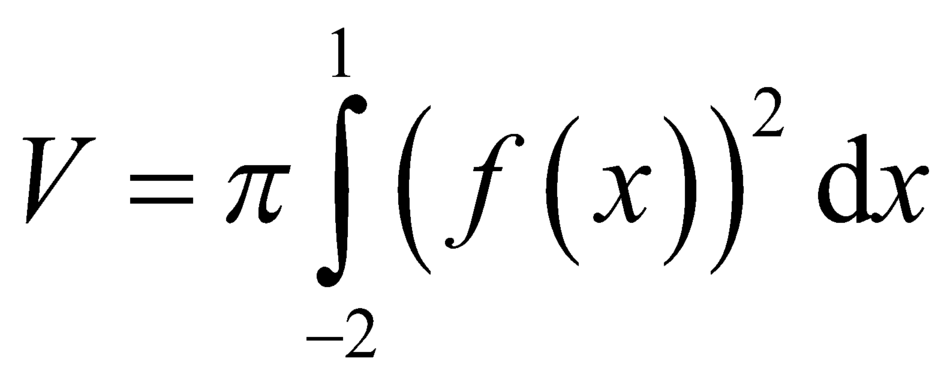
Cho hình phẳng (H) giới hạn bởi trục hoành, đồ thị của một parabol và một đường thẳng tiếp xúc parabol đó tại điểm A(2;4) như hình vẽ bên. Tính thể tích khối tròn xoay tạo bởi hình phẳng (H) khi quay xung quanh trục Ox. A.
32
π
5
B.
16
π
15
C.
22
π...
Đọc tiếp
Cho hình phẳng (H) giới hạn bởi trục hoành, đồ thị của một parabol và một đường thẳng tiếp xúc parabol đó tại điểm A(2;4) như hình vẽ bên. Tính thể tích khối tròn xoay tạo bởi hình phẳng (H) khi quay xung quanh trục Ox.
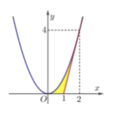
A. 32 π 5
B. 16 π 15
C. 22 π 5
D. 2 π 3