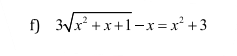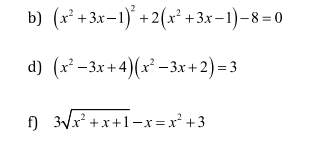Lời giải:
Đặt $\sqrt[3]{2x+1}=a; \sqrt[3]{x}=b$ thì ta có:
$a+b=1$ và $a^3-2b^3=1$
$\Rightarrow a^3-2b^3=(a+b)^3$
$\Leftrightarrow a^3-2b^3=a^3+3a^2b+3ab^2+b^3$
$\Leftrightarrow 3a^2b+3ab^2+3b^3=0$
$\Leftrightarrow b(a^2+ab+b^2)=0$
$\Leftrightarrow b=0$ hoặc $a^2+ab+b^2=0$
Nếu $b=0\Leftrightarrow \sqrt[3]{x}=0\Leftrightarrow x=0$ (thử lại thấy tm)
Nếu $a^2+ab+b^2=0$
$\Leftrightarrow (a+\frac{b}{2})^2+\frac{3}{4}b^2=0$
$\Rightarrow a+\frac{b}{2}=b=0$
$\Rightarrow a=b=0$
$\Leftrightarrow \sqrt[3]{2x+1}=\sqrt[3]{x}=0$
$\Leftrightarrow x=\frac{-1}{2}=0$ (vô lý)
Vậy $x=0$

 p
p