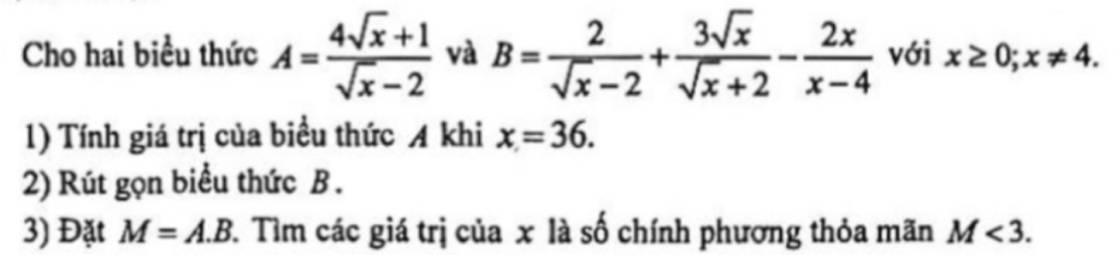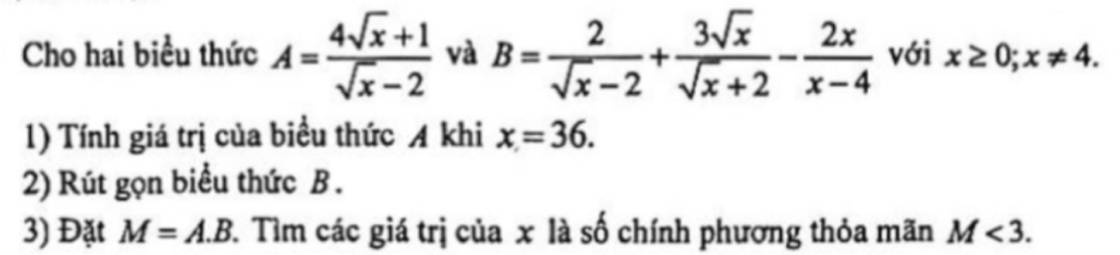1: Khi x=36 thì \(A=\dfrac{4\cdot6+1}{6-2}=\dfrac{25}{4}\)
2: \(B=\dfrac{2}{\sqrt{x}-2}+\dfrac{3\sqrt{x}}{\sqrt{x}+2}-\dfrac{2x}{x-4}\)
\(=\dfrac{2\left(\sqrt{x}+2\right)+3\sqrt{x}\left(\sqrt{x}-2\right)-2x}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{2\sqrt{x}+4+3x-6\sqrt{x}-2x}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x-4\sqrt{x}+4}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}=\dfrac{\left(\sqrt{x}-2\right)^2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}-2}{\sqrt{x}+2}\)
3: M=A*B
\(=\dfrac{\sqrt{x}-2}{\sqrt{x}+2}\cdot\dfrac{4\sqrt{x}+1}{\sqrt{x}-2}\)
\(=\dfrac{4\sqrt{x}+1}{\sqrt{x}+2}\)
M<3
=>M-3<0
=>\(\dfrac{4\sqrt{x}+1-3\sqrt{x}-6}{\sqrt{x}+2}< 0\)
=>\(\dfrac{\sqrt{x}-5}{\sqrt{x}+2}< 0\)
=>\(\sqrt{x}-5< 0\)
=>\(\sqrt{x}< 5\)
=>0<=x<25
Kết hợp ĐKXĐ, ta được: \(\left\{{}\begin{matrix}0< =x< 25\\x< >4\end{matrix}\right.\)
mà x là số chính phương
nên \(x\in\left\{0;1;9;16\right\}\)