- Dùng SLT
- Dùng đồng vị
- Dùng TCP
- Dùng SLN
- Dùng NCP
Tham Khảo
I. Lý thuyết liên quan đến hai đường thẳng song song
1. Khoảng cách giữa hai đường thẳng song song
Khoảng cách giữa hai đường thẳng song song là khoảng cách từ một điểm tùy ý trên đường thằng này đến đường thẳng kia.
2. Tính chất của các điểm các đều một đường thẳng cho trước
Các điểm cách đều một đường thẳng b một khoảng là h nằm trên hai đường thẳng song song với b và cách b một khoảng bằng h.
Nhận xét: Tập hớp các điểm cách một đường thẳng cố định một khoảng cách bằng h không đổi là hai đường thẳng song song với đường thẳng đó và cách đường thẳng đó một khoảng bằng h.
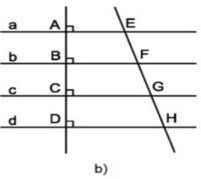
3. Đường thẳng song song cách đều
Cho các đường thẳng a, b, c, d song song với nhau và khoảng cách giữa các đường thẳng a và b, b và c, c và d bằng nhau. Khi đó ta gọi a, b, c, d là các đường thẳng song song cách đều.
Ta có định lí:
– Nếu các đường thẳng song song cách đều cắt một đường thẳng thì chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau.
– Nếu các đường thẳng song song cắt một đường thẳng và chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau thì chúng song song cách đều.
Cái này cope trên mạng :)
+Xét vị trí các cặp góc tạo bởi hai đường thẳng định chứng minh song song với một đường thẳng thứ ba (so le, đồng vị…)
+Sử dụng tính chất của hình bình hành.
+Hai đường thẳng cùng song song hoặc cùng vuông góc với đường thẳng thứ ba.
+Sử dụng tính chất đường trung bình của tam giác, hình thang, hình bình hành.
+Sử dụng định nghĩa hai đường thẳng song song.
+Sử dụng kết quả của các đoạn thẳng tương ứng tỉ lệ để suy ra các đường thẳng song song tương ứng.
+Sử dụng tính chất của đường thẳng đi qua trung điểm hai cạnh bên hay đi qua trung điểm của hai đường chéo của hình thang.
+Sử dụng tính chất hai cung bằng nhau của một đường tròn.
+Sử dụng phương pháp chứng minh bằng phản chứng.
- so le trong
- đồng vị =
- trong cùng phía bù nhau
- 2 đg thẳng vuông góc vs 1 đg thẳng
...............