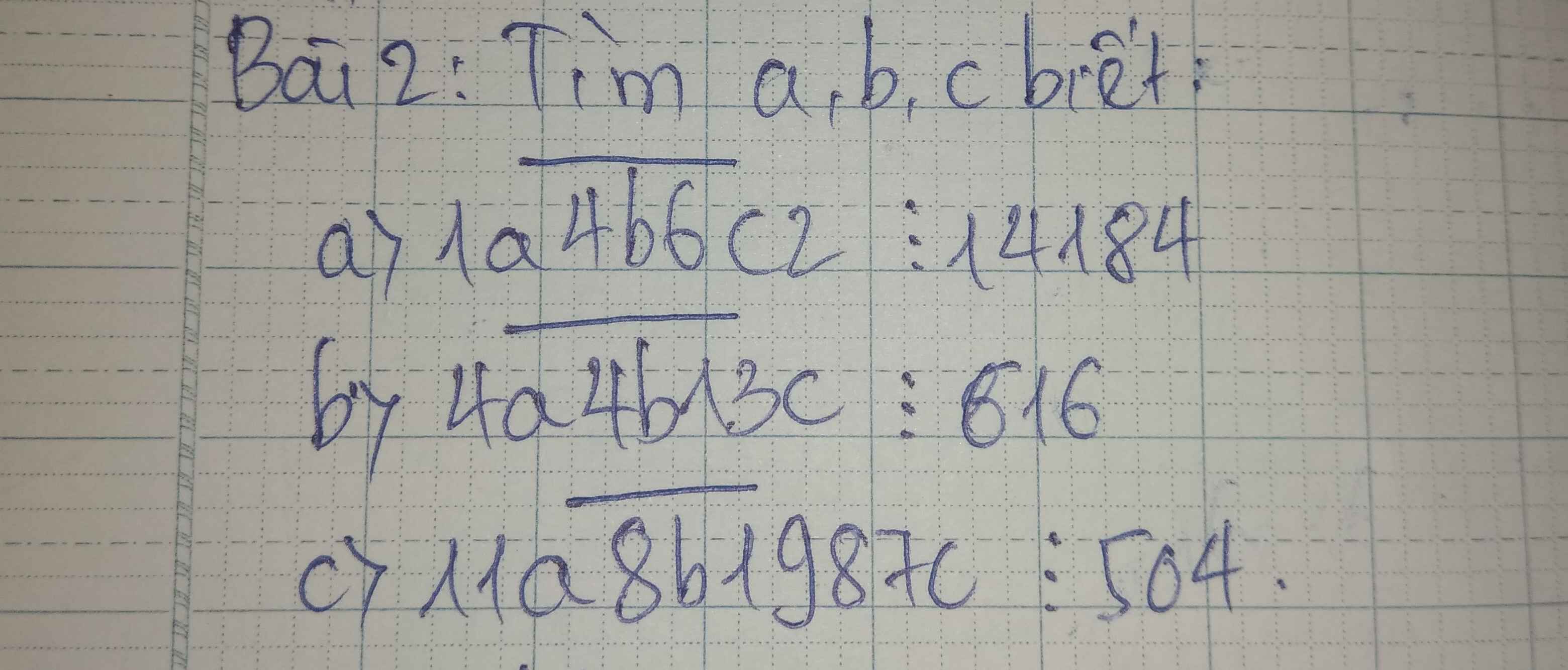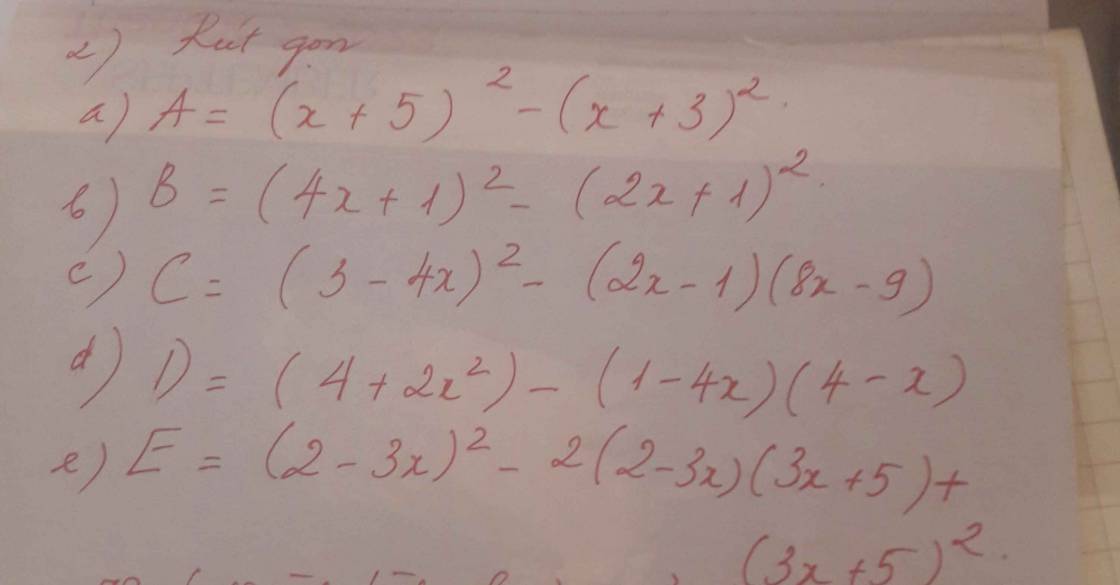Bài 2:
a) Ta có: AB=AD(gt)
nên A nằm trên đường trung trực của BD(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: CB=CD(gt)
nên C nằm trên đường trung trực của BD(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AC là đường trung trực của BD(Đpcm)
b) Ta có: \(\widehat{BCD}=60^0\)
nên \(\widehat{CBD}=\widehat{CDB}=60^0\)
Ta có: \(\widehat{BAD}=100^0\)
nên \(\widehat{ABD}=\widehat{ADB}=\dfrac{180^0-100^0}{2}=\dfrac{80^0}{2}=40^0\)
\(\Leftrightarrow\widehat{ABC}=100^0;\widehat{ADC}=100^0\)








 nhờ mng giúp ạ
nhờ mng giúp ạ