Bốn cạnh bằng nhau
Bốn góc bằng nhau
Hai đường chéo bằng nhau
Hai đường chéo là đường trung trực của nhau
Hai đường chéo là hai đường phân giác của 4 góc trong hình vuông
Trên mặt phẳng, cho hình vuông có cạnh bằng 2. Chọn ngẫu nhiên một điểm thuộc hình vuông đã cho (kể cả các điểm nằm trên cạnh của hình vuông). Gọi P là xác suất để điểm được chọn thuộc vào hình tròn nội tiếp hình vuông đã cho (kể cả các điểm nằm trên đường tròn nội tiếp hình vuông), giá trị gần nhất của P là
Nêu hai tính chất đặc trưng của hình đa diện
Cho hình chóp có đáy là hình vuông tâm O, cạnh bằng 4a. Cạnh bên SA = 2a. Hình chiếu vuông góc của đỉnh S trên mặt phẳng là trung điểm của H của đoạn thẳng AO. Tính khoảng cách d giữa các đường thẳng SD và AB.
A. d = 4a.
B. d = 4 a 22 11
C. d = 2a
D. d = 3 a 2 11
Trong không gian Oxyz, cho điểm A(2;-3;4). Lập phương trình mặt phẳng (P) đi qua các hình chiếu vuông góc của điểm A trên các trục tọa độ:
A. 2x-3y+4z-29=0
B. 2x-3y+4z-1=0
C. x 2 + y - 3 + z 4 = 0
D. x 2 + y - 3 + z 4 = 1
Cho hình vuông A 1 B 1 C 1 D 1 có cạnh bằng 1. Gọi A k + 1 , B k + 1 , C k + 1 , D k + 1 theo thứ tự là trung điểm của các cạnh A k B k , B k C k , C k D k , D k A k (với k = 1 , 2 , ... ). Chu vi của hình vuông A 2018 B 2018 C 2018 D 2018 bằng
A. 2 2 1007
B. 2 2 1006
C. 2 2 2017
D. 2 2 2018
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Gọi M và N lần lượt là trung điểm của các cạnh AB và AD; H là giao điểm của CN và DM. Biết SH vuông góc với mặt phẳng (ABCD) và SH = a 3 . Tính thể tích khối chóp S.CDNM theo a.
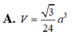
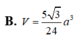
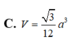
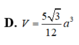
Cho các tập hợp : A = 
; B = A \
;
Biểu diễn A, B bằng cách nêu tính chất đặc trưng của các phần tử
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Gọi M, N lần lượt là trung điểm của các cạnh AB, AD; H là giao điểm của CN với DM. Biết SH vuông góc với mặt phẳng (ABCD) và SH= a 3 . Tính khoảng cách giữa hai đường thẳng DM và SC theo a.
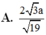
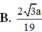
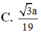
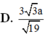
Cho ba điểm A, B, C thẳng hang theo thứ tự đó và AB = 2BC. Dựng các hình vuông ABEF, BCGH (đỉnh của hình vuông tính theo chiều kim đồng hồ). Xét phép quay tâm B góc quay - 90 ° biến điểm E thành điểm A. Gọi I là giao điểm của EC và GH. Giả sử I biến thành điểm J qua phép quay trên. Nếu AC = 3 thì IJ bằng bao nhiêu?
A. 10 2
B. 5
C. 2 5
D. 10
