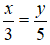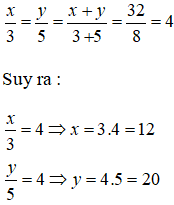Gọi cd,cr ll là a,b(cm;a,b>0)
Áp dụng tc dtsbn:
\(\dfrac{a}{5}=\dfrac{b}{3}=\dfrac{2\left(a+b\right)}{2\left(5+3\right)}=\dfrac{64}{16}=4\\ \Rightarrow\left\{{}\begin{matrix}a=20\\b=12\end{matrix}\right.\)
Vậy...
Gọi chiều dài, chiều rộng lần lượt là a,b (a,b>0)
Theo bài ra ta có:\(\left\{{}\begin{matrix}a+b=64:2=32\left(cm\right)\\\dfrac{a}{5}=\dfrac{b}{3}\end{matrix}\right.\)
Áp dụng t/c dtsbn ta có:
\(\dfrac{a}{5}=\dfrac{b}{3}=\dfrac{a+b}{5+3}=\dfrac{32}{8}=4\)
\(\dfrac{a}{5}=4\Rightarrow a=20\\ \dfrac{b}{3}=4\Rightarrow b=12\)
Tham khảo!
Gọi x, y (cm) lần lượt là chiều rộng và chiều dài của hình chữ nhật (y > x > 0)
Nửa chu vi của hình chữ nhật là: 64 : 2 = 32 (cm)
Do đó: x + y = 32.
Do chiều rộng và chiều dài của hình chữ nhật tỉ lệ với 3 và 5 nên ta có:
Theo tính chất của dãy số tỉ số bằng nhau ta có:
=>Chiều rộng 12cm
=> Chiều dài 20cm
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{5}=\dfrac{b}{3}=\dfrac{a+b}{5+3}=\dfrac{32}{8}=4\)
Do đó: a=20; b=12