Theo quy tắc nhân có mn cách.
Chọn đáp án C.
Theo quy tắc nhân có mn cách.
Chọn đáp án C.
Cho hàm số y = x 3 - m x + 1 - m có đồ thị C m . Gọi M là điểm có hoành độ bằng 0 và thuộc C m . Tìm tất cả các giá trị thực của tham số m để tiếp tuyến của C m tại M cắt trục hoành tại N sao cho MN = 2 2
A. m ∈ - 1 ; 3 ± 2 2
B. m ∈ - 1 ; 2 ± 3
C. m ∈ 1 ; - 3 ± 2 2
D. m ∈ 1 ; 2 ± 3
Gọi M là điểm có hoành độ khác 0, thuộc đồ thị (C) của hàm số y = x 3 - 3 x . Tiếp tuyến của (C) tại M cắt (C) tại điểm thứ hai là N (N không trùng với M). Kí hiệu x M , x N thứ tự là hoành độ của M và N. Kết luận nào sau đây là đúng?
A. 2 x M + x N = 0
B. x M + 2 x N = 3
C. x M + x N = - 2
D. x M + x N = 3
Một con đường được xây dựng giữa hai thành phố A, B. Hai thành phố này bị ngăn cách bởi một con sông có chiều rộng r(m). Người ta cần xây 1 cây cầu bắc qua sông biết rằng A cách con sông một khoảng bằng 2m, B cách con sông một khoảng bằng 4m. Để tổng khoảng cách giữa các thành phố là nhỏ nhất thì giá trị x(m) bằng
A. 2
B. 4
C. 3
D. 1
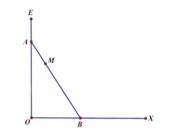
Trên một đoạn đường giao thông có hai con đường vuông góc với nhau tại O như hình vẽ. Một địa danh lịch sử có vị trí đặt tạiM, vị trí M cách đường OE 125 m và cách đường OX 1km. Vì lý do thực tiễn người ta muốn làm một đoạn đường thẳng AB đi qua vị trí M, biết rằng giá trị để làm 100m đường là 150 triệu đồng. Chọn vị trí của A và B để hoàn thành con đường với chi phí thấp nhất. Hỏi chi phí thấp nhất để hoàn thành con đường là bao nhiêu?
A. 2,3965 tỷ đồng
B. 1,9063 tỷ đồng
C. 3,0264 tỷ đồng
D. 2,0963 tỷ đồng
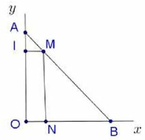
Trên một đoạn đường giao thông có hai con đường vuông góc với nhau tại O như hình vẽ. Một địa danh có vị trí đặt tại M, vị trí M cách đường Oy 216m và cách đường Ox 1000m. Vì lý do thực tiễn, người ta muốn làm một đoạn đường thẳng AB đi qua vị trí M, biết rằng giá để làm 100m đường là 200 triệu đồng. Chọn vị trí A và B để hoàn thành con đường với chi phí thấp nhất. Hỏi chi phí thấp nhất để hoàn thành con đường là bao nhiêu?
A. 2,093 tỷ đồng
B. 2,153 tỷ đồng
C. 1,967 tỷ đồng
D. 3,172 tỷ đồng
Trên một đoạn đường giao thông có hai con đường vuông góc với nhau tại O như hình vẽ. Một địa danh có vị trí đặt tại M , vị trí M cách đường Oy 216m và cách đường Ox 1000m. Vì lý do thực tiễn, người ta muốn làm một đoạn đường thẳng AB đi qua vị trí M, biết rằng giá để làm 100m đường là 200 triệu đồng. Chọn vị trí của A và B để hoàn thành con đường với chi phí thấp nhất. Hỏi chi phí thấp nhất để hoàn thành con đường là bao nhiêu?
A. 2,093 tỷ đồng
B. 3,172 tỷ đồng
C. 1,967 tỷ đồng
D. 2,153 tỷ đồng
Cho hàm số y = x 4 − 2 m x 2 + m C với m là tham số thực. Gọi A là điểm thuộc đồ thị (C) có hoành độ bằng 1. Tìm tham số m để tiếp tuyến ∆ với đồ thị (C) tại A cắt đường tròn T : x 2 + y − 1 2 = 4 tạo thành một dây cung có độ dài nhỏ nhất
A. m = 16 13
B. m = - 13 16
C. m = 13 16
D. m = − 16 13
Cho hàm số y = 4 x = 3 x - 3 có đồ thị (C). Biết đồ thị (C) có hai điểm phân biệt M, N và khoảng cách từ M hoặc N đến hai đường tiệm cận là nhỏ nhất. Khi đó MN có giá trị bằng:
A. MN = 6
B. MN = 4 2
C. MN = 6 2
D. MN = 4 3
Sau 1 tháng thi công thì công trình xây dựng Nhà học thể dục của trường X đã thực hiện được một khối lượng công việc. Nếu tiếp tục với tiến độ như vậy thì dự kiến sau đúng 23 tháng nữa công trình sẽ hoàn thành. Để sớm hoàn thành công trình và kịp đưa vào sử dụng, công ty xây dựng quyết định từ tháng thứ 2, mỗi tháng tăng 4% khối lượng công việc so với tháng kề trước. Hỏi công trình sẽ hoàn thành ở tháng thứ mấy sau khi khởi công?
A. 19
B. 18
C. 17
D. 20