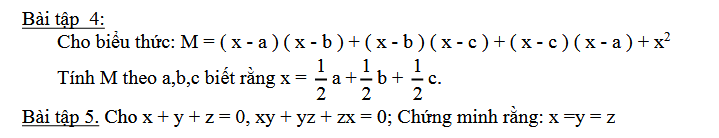a) Ta có: \(\left(3x+1\right)^3\)
\(=\left(3x\right)^3+3\cdot\left(3x\right)^2\cdot1+3\cdot3x\cdot1^2+1^3\)
\(=27x^3+27x^2+9x+1\)
b) Ta có: \(\left(2x-\dfrac{1}{x}\right)^3\)
\(=\left(2x\right)^3-3\cdot\left(2x\right)^2\cdot\dfrac{1}{x}+3\cdot2x\cdot\left(\dfrac{1}{x}\right)^2-\left(\dfrac{1}{x}\right)^3\)
\(=8x^3-12x+\dfrac{6}{x}-\dfrac{1}{x^3}\)
c) Ta có: \(\left(y-\dfrac{xy}{3}\right)^3\)
\(=y^3-3y^2\cdot\dfrac{xy}{3}+3y\cdot\left(\dfrac{xy}{3}\right)^2-\left(\dfrac{xy}{3}\right)^3\)
\(=y^3-xy^3+\dfrac{x^2y^3}{3}-\dfrac{x^3y^3}{27}\)
d) Ta có: \(\left(\dfrac{1}{y^2}+\dfrac{y}{x}\right)^3\)
\(=\left(\dfrac{1}{y^2}\right)^3+3\cdot\dfrac{1}{y^4}\cdot\dfrac{y}{x}+3\cdot\dfrac{1}{y^2}\cdot\dfrac{y^2}{x^2}+\left(\dfrac{y}{x}\right)^3\)
\(=\dfrac{1}{y^6}+\dfrac{3y^3}{x}+\dfrac{3}{x^2}+\dfrac{y^3}{x^3}\)


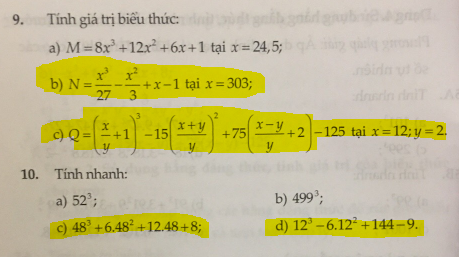 Mọi người ơi giúp em với ạ. Mai em phải nộp rồi. Mấy phần em đánh dấu đó mọi người.
Mọi người ơi giúp em với ạ. Mai em phải nộp rồi. Mấy phần em đánh dấu đó mọi người. 


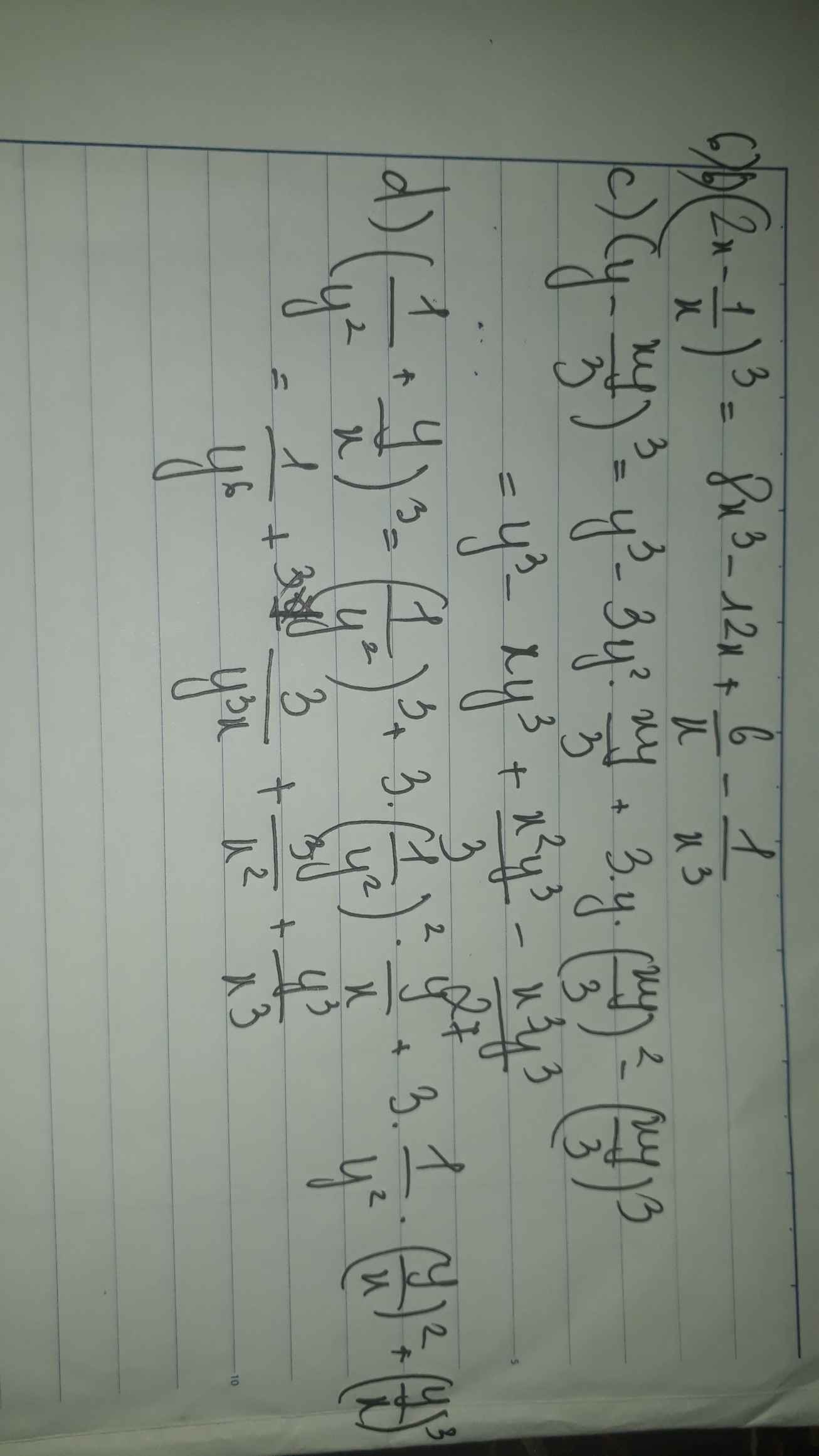
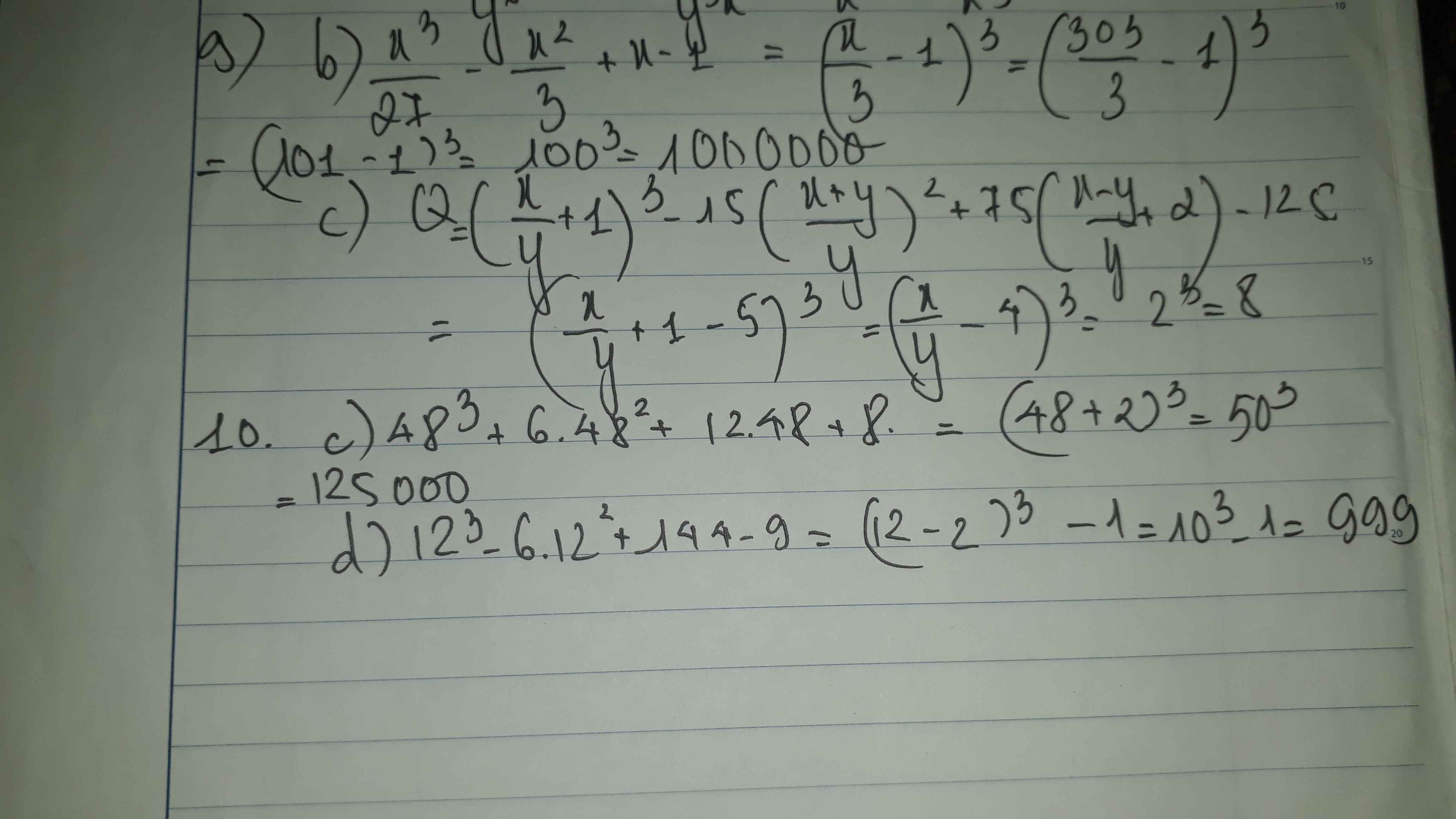


 Mọi người cứu em, tối nay phải nộp rồi.
Mọi người cứu em, tối nay phải nộp rồi.