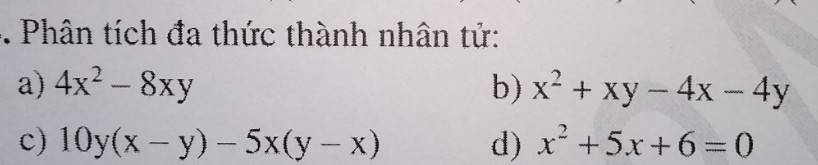\(a,4x^2-8xy=4x\left(x-2y\right)\)
\(b,x^2+xy-4x-4y=x\left(x+y\right)-4\left(x+y\right)=\left(x+y\right)\left(x-4\right)\)
\(c,10y\left(x-y\right)-5x\left(y-x\right)=10y\left(x-y\right)+5x\left(x-y\right)=\left(x-y\right)\left(10y+5x\right)\)
\(d,x^2+5x+6=0\)
\(\Rightarrow x^2+2x+3x+6=0\)
\(\Rightarrow x\left(x+2\right)+3\left(x+2\right)=0\)
\(\Rightarrow\left(x+2\right)\left(x+3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x+2=0\\x+3=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=-2\\x=-3\end{matrix}\right.\)
Vậy \(x\in\left\{-2;-3\right\}\)
a)
\(4x^2-8xy\)
\(=4x\left(x-2y\right)\)
b)
\(=x\left(x+y\right)-\left(4x+4y\right)\)
\(=x\left(x+y\right)-4\left(x+y\right)\)
\(=\left(x+y\right)\left(x-4\right)\)
c)
\(=10y\left(x-y\right)+5x\left(x-y\right)\)
\(=\left(x-y\right)\left(10y+5x\right)=5\left(x-y\right)\left(2y+x\right)\)
d)
\(x^2+5x+6=0< =>x^2+3x+2x+6=0< =>x\left(x+3\right)+2\left(x+3\right)=0< =>\left(x+3\right)\left(x+2\right)=0< =>\left[{}\begin{matrix}x+3=0\\x+2=0\end{matrix}\right.< =>\left[{}\begin{matrix}x=-3\\x=-2\end{matrix}\right.\)
a) \(4x^2-8xy=4x\left(x-2y\right)\)
b)\(x^2+xy-4x-4y=x\left(x+y\right)-4\left(x+y\right)=\left(x-4\right)\left(x+y\right)\)
c)\(10y\left(x-y\right)-5x\left(y-x\right)=10y\left(x-y\right)+5x\left(x-y\right)=\left(10y+5x\right)\left(x-y\right)=5\left(2y+x\right)\left(x-y\right)\) d)\(x^2+5x+6=x^2+2x+3x+6=x\left(x+2\right)+3\left(x+2\right)=\left(x+3\right)\left(x+2\right)\)