a: ΔOBC cân tại O
mà OI là đường trung tuyến
nên OI\(\perp\)BC tại I
Xét tứ giác AION có \(\widehat{AIO}+\widehat{ANO}=90^0+90^0=180^0\)
nên AION là tứ giác nội tiếp
=>A,I,O,N cùng thuộc một đường tròn
b: Xét (O) có
\(\widehat{AMB}\) là góc tạo bởi tiếp tuyến MA và dây cung MB
\(\widehat{MCB}\) là góc nội tiếp chắn cung MB
Do đó: \(\widehat{AMB}=\widehat{MCB}\)
Xét ΔAMB và ΔACM có
\(\widehat{AMB}=\widehat{ACM}\)
\(\widehat{MAB}\) chung
Do đó: ΔAMB~ΔACM
=>\(\dfrac{AM}{AB}=\dfrac{AC}{AM}\)
=>\(AC=\dfrac{AM\cdot AM}{AB}=\dfrac{AM^2}{AB}\)
Xét (O) có
AM,AN là các tiếp tuyến
DO đó: AM=AN
=>A nằm trên đường trung trực của MN(1)
Ta có: OM=ON
=>O nằm trên đường trung trực của NM(2)
Từ (1),(2) suy ra OA là đường trung trực của MN
=>OA\(\perp\)MN tại K
Xét ΔAMO vuông tại M có MK là đường cao
nên \(AK\cdot AO=AM^2\)
=>\(AK\cdot AO=AB\cdot AC\)
=>\(\dfrac{AK}{AC}=\dfrac{AB}{AO}\)
Xét ΔAKB và ΔACO có
\(\dfrac{AK}{AC}=\dfrac{AB}{AO}\)
\(\widehat{KAB}\) chung
Do đó: ΔAKB~ΔACO
=>\(\widehat{AKB}=\widehat{ACO}\)
mà \(\widehat{AKB}+\widehat{OKB}=180^0\)(hai góc kề bù)
nên \(\widehat{OKB}+\widehat{OCB}=180^0\)
=>BKOC là tứ giác nội tiếp
=>\(\widehat{BOC}=\widehat{BKC}\)
a: ΔOBC cân tại O
mà OI là đường trung tuyến
nên OI\(\perp\)BC tại I
Xét tứ giác AION có \(\widehat{AIO}+\widehat{ANO}=90^0+90^0=180^0\)
nên AION là tứ giác nội tiếp
=>A,I,O,N cùng thuộc một đường tròn
b: Xét (O) có
\(\widehat{AMB}\) là góc tạo bởi tiếp tuyến MA và dây cung MB
\(\widehat{MCB}\) là góc nội tiếp chắn cung MB
Do đó: \(\widehat{AMB}=\widehat{MCB}\)
Xét ΔAMB và ΔACM có
\(\widehat{AMB}=\widehat{ACM}\)
\(\widehat{MAB}\) chung
Do đó: ΔAMB~ΔACM
=>\(\dfrac{AM}{AB}=\dfrac{AC}{AM}\)
=>\(AC=\dfrac{AM\cdot AM}{AB}=\dfrac{AM^2}{AB}\)
Xét (O) có
AM,AN là các tiếp tuyến
DO đó: AM=AN
=>A nằm trên đường trung trực của MN(1)
Ta có: OM=ON
=>O nằm trên đường trung trực của NM(2)
Từ (1),(2) suy ra OA là đường trung trực của MN
=>OA\(\perp\)MN tại K
Xét ΔAMO vuông tại M có MK là đường cao
nên \(AK\cdot AO=AM^2\)
=>\(AK\cdot AO=AB\cdot AC\)
=>\(\dfrac{AK}{AC}=\dfrac{AB}{AO}\)
Xét ΔAKB và ΔACO có
\(\dfrac{AK}{AC}=\dfrac{AB}{AO}\)
\(\widehat{KAB}\) chung
Do đó: ΔAKB~ΔACO
=>\(\widehat{AKB}=\widehat{ACO}\)
mà \(\widehat{AKB}+\widehat{OKB}=180^0\)(hai góc kề bù)
nên \(\widehat{OKB}+\widehat{OCB}=180^0\)
=>BKOC là tứ giác nội tiếp
=>\(\widehat{BOC}=\widehat{BKC}\)







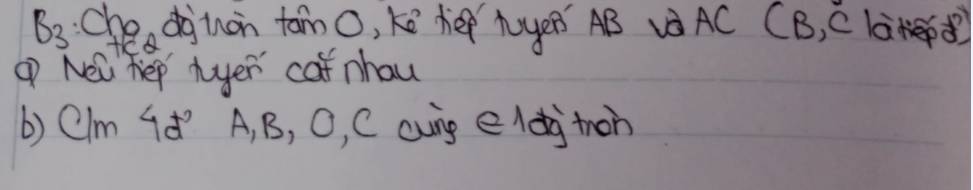

 vẽ hình giúp mik nx nha
vẽ hình giúp mik nx nha













 bài 2
bài 2 giúp mik hai bài này với (kẻ bảng nx nha ) cảm ưn nhiều
giúp mik hai bài này với (kẻ bảng nx nha ) cảm ưn nhiều