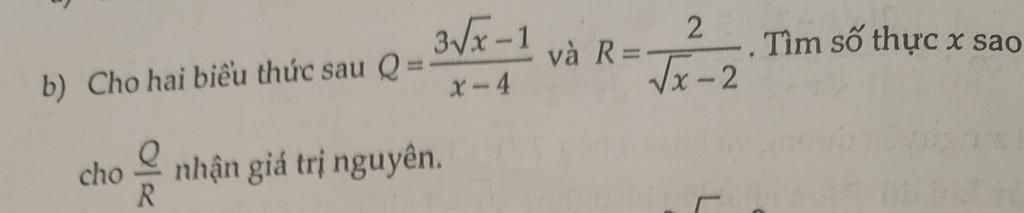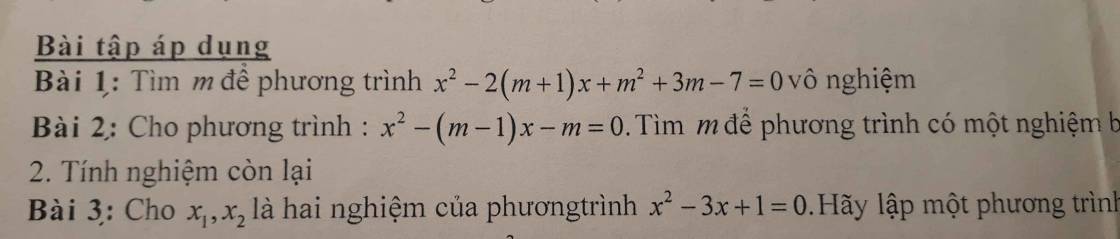\(P=\dfrac{Q}{R}=\dfrac{3\sqrt{x}-1}{x-4}:\dfrac{2}{\sqrt{x}-2}\)
\(=\dfrac{3\sqrt{x}-1}{x-4}\cdot\dfrac{\sqrt{x}-2}{2}=\dfrac{3\sqrt{x}-1}{2\sqrt{x}+4}\)
P là số nguyên
=>\(3\sqrt{x}-1⋮2\sqrt{x}+4\)
=>\(6\sqrt{x}-2⋮2\sqrt{x}+4\)
=>\(6\sqrt{x}+12-14⋮2\sqrt{x}+4\)
=>\(2\sqrt{x}+4\inƯ\left(-14\right)\)
mà 2*căn x+4>=4
nên \(2\sqrt{x}+4\in\left\{7;14\right\}\)
=>\(2\sqrt{x}\in\left\{3;10\right\}\)
=>\(x\in\left\{\dfrac{9}{4};25\right\}\)
Ta có:
\(\dfrac{Q}{R}\) là:
\(\dfrac{3\sqrt{x}-1}{x-4}:\dfrac{2}{\sqrt{x}-2}\) (ĐK: \(x\ge0;x\ne4\))
\(=\dfrac{3\sqrt{x}-1}{\left(\sqrt{x}\right)^2-2^2}:\dfrac{2}{\sqrt{x}-2}\)
\(=\dfrac{3\sqrt{x}-1}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\cdot\dfrac{\sqrt{x}-2}{2}\)
\(=\dfrac{\left(3\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}{2\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{3\sqrt{x}-1}{2\left(\sqrt{x}+2\right)}\)
\(=\dfrac{3\sqrt{x}-1}{2\sqrt{x}+4}\)
Để giá trị của biểu thức \(\dfrac{Q}{R}\) nguyên thì
\(3\sqrt{x}-1\) chia hết cho \(2\sqrt{x}+4\)
⇒ \(2\left(3\sqrt{x}-1\right)\) chia hết cho \(2\sqrt{x}+4\)
⇒ \(6\sqrt{x}-2\) chia hết cho \(2\sqrt{x}+4\)
⇒ \(6\sqrt{x}+12-14\) chia hết cho \(2\sqrt{x}+4\)
⇒ \(3\left(2\sqrt{x}+4\right)-14\) chia hết cho \(2\sqrt{x}+4\)
⇒ - 14 chia hết cho \(2\sqrt{x}+4\)
Mà: Ư(-14)\(=\left\{1;-1;2;-2;7;-7;14;-14\right\}\)
ĐK: \(2\sqrt{x}+4\ge4\)
\(\Rightarrow2\sqrt{x}+4\in\left\{7;14\right\}\)
\(\Rightarrow x\in\left\{\dfrac{9}{4};25\right\}\)