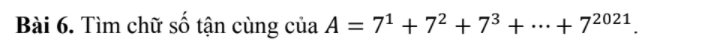Lời giải:
$A=7+(7^2+7^3+7^4+7^5)+(7^6+7^6+7^8+7^9)+....+(7^{2018}+7^{2019}+7^{2020}+7^{2021})$
$=7+7^2(1+7+7^2+7^3)+7^6(1+7+7^2+7^3)+....+7^{2018}(1+7+7^2+7^3)$
$=7+(1+7+7^2+7^3)(7^2+7^6+....+7^{2018}$
$=7+400(7^2+7^6+....+7^{2018})$
Dễ thấy $400(7^2+7^6+....+7^{2018})$ tận cùng là $0$
Do đó $A$ tận cùng là $7$
Đúng 0
Bình luận (0)