2) Ta có: \(\left|4-3x\right|=\left|x+\dfrac{1}{3}\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}4-3x=x+\dfrac{1}{3}\\3x-4=x+\dfrac{1}{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}-4x=-\dfrac{11}{3}\\2x=\dfrac{13}{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{11}{12}\\x=\dfrac{13}{6}\end{matrix}\right.\)
3: Ta có: \(\left|5x-2\right|-\left|3x+\dfrac{1}{2}\right|=0\)
\(\Leftrightarrow\left|5x-2\right|=\left|3x+\dfrac{1}{2}\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}5x-2=3x+\dfrac{1}{2}\\5x-2=-3x-\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{5}{2}\\8x=\dfrac{3}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{4}\\x=\dfrac{3}{16}\end{matrix}\right.\)
4: Ta có: \(\left|2x-1\right|=x+\dfrac{4}{3}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=x+\dfrac{4}{3}\left(x\ge\dfrac{1}{2}\right)\\1-2x=x+\dfrac{4}{3}\left(x< \dfrac{1}{2}\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x-x=\dfrac{4}{3}+1\\-2x-x=\dfrac{4}{3}-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7}{3}\\-3x=\dfrac{1}{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7}{3}\\x=-\dfrac{1}{9}\end{matrix}\right.\)
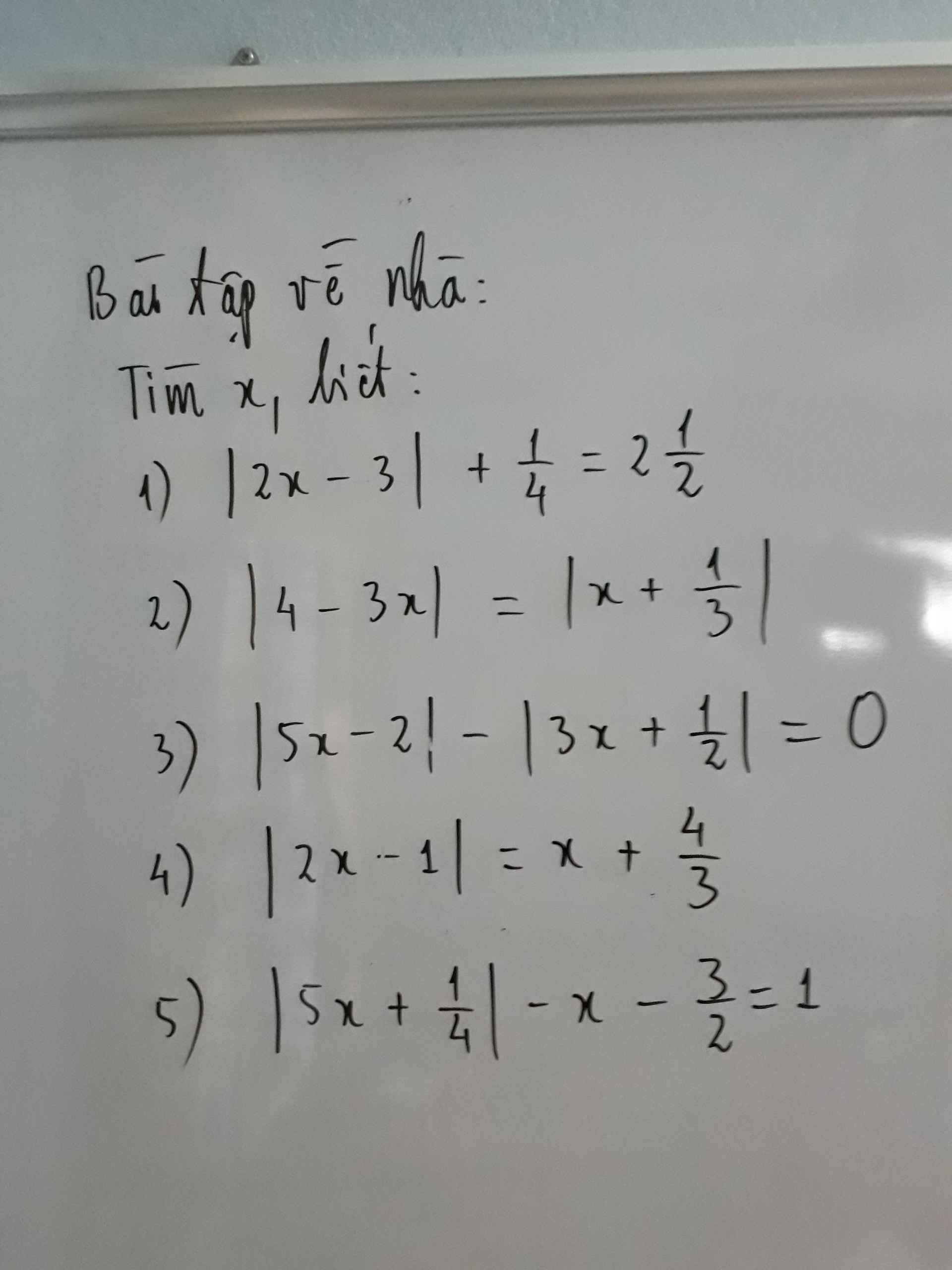
lm giúp mk bài 3 với bài 4 với ạ, mk đng cần gấp, cảm ơn mn rất rất nhiều ạ !!!!
