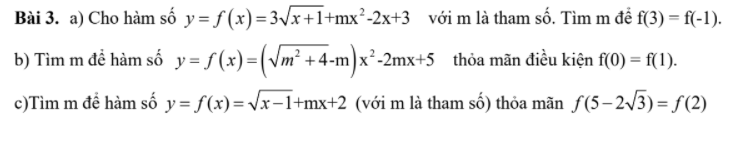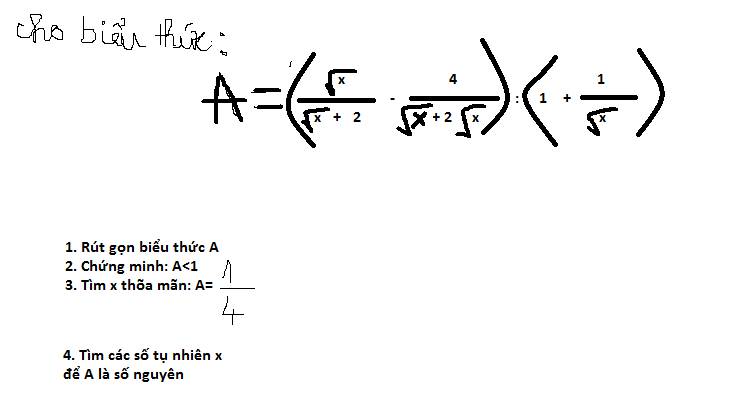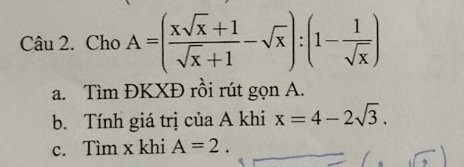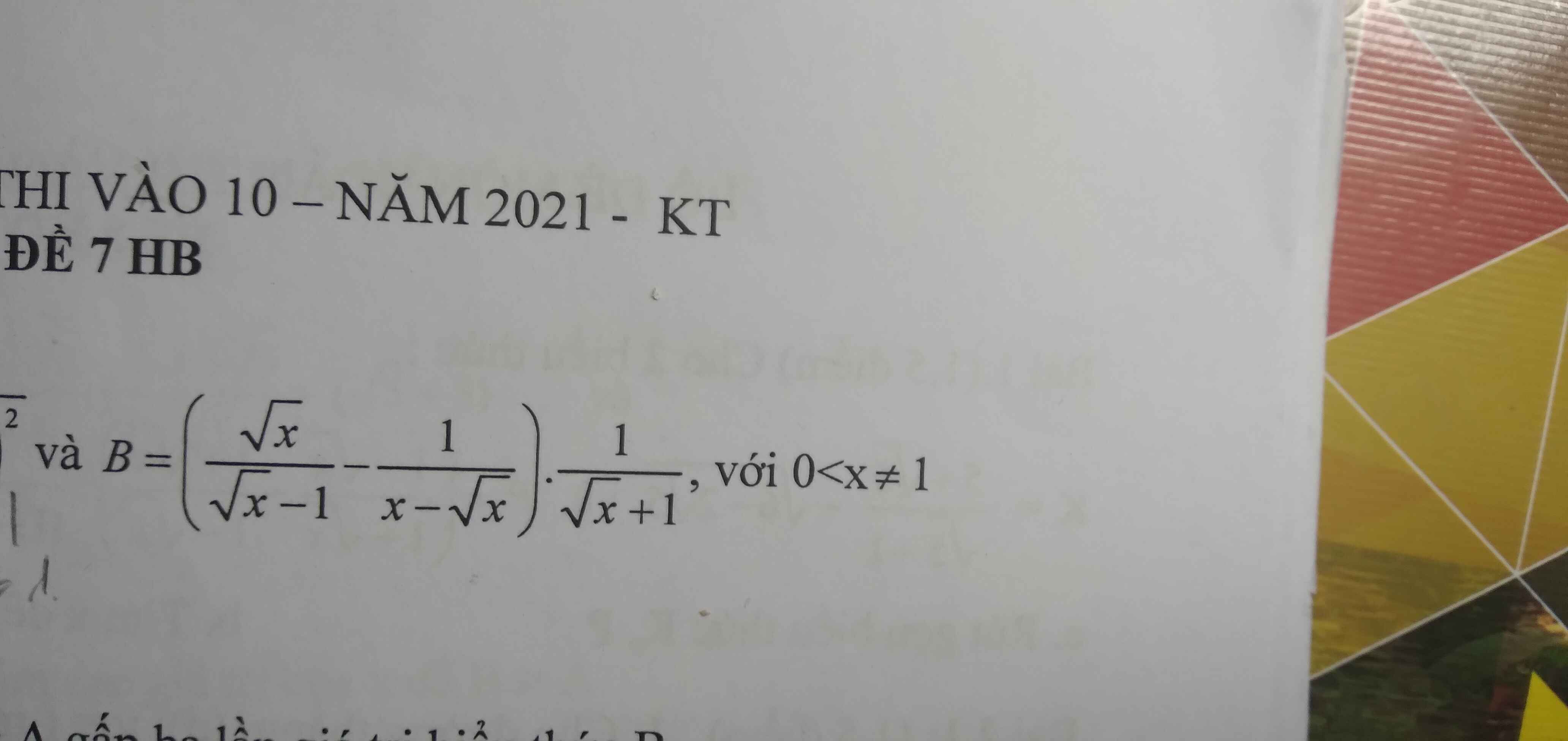b) \(2x^3+x^2+x=\left(x^2+6x+6\right)\sqrt{x+1}\left(x\ge-1\right)\)
\(\Leftrightarrow\left(2x^3+x^2+x\right)^2=\left[\left(x^2+6x+6\right)\sqrt{x+1}\right]^2\)
\(\Leftrightarrow x^2\left(2x^2+x+1\right)^2=\left(x^2+6x+6\right)^2\left(x+1\right)\)
\(\Leftrightarrow4x^6+4x^5+5x^4+2x^3+x^2=x^5+13x^4+60x^3+120x^2+108x+36\)
\(\Leftrightarrow4x^6+3x^5-8x^4-58x^3-119x^2-108x-36=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\left(tm\right)\\x=-\dfrac{3}{4}\left(tm\right)\end{matrix}\right.\)
Vậy nghiệm của phương trình cho là \(x\in\left\{-\dfrac{3}{4};3\right\}\)
Đúng 0
Bình luận (0)
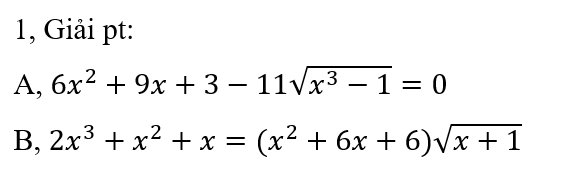
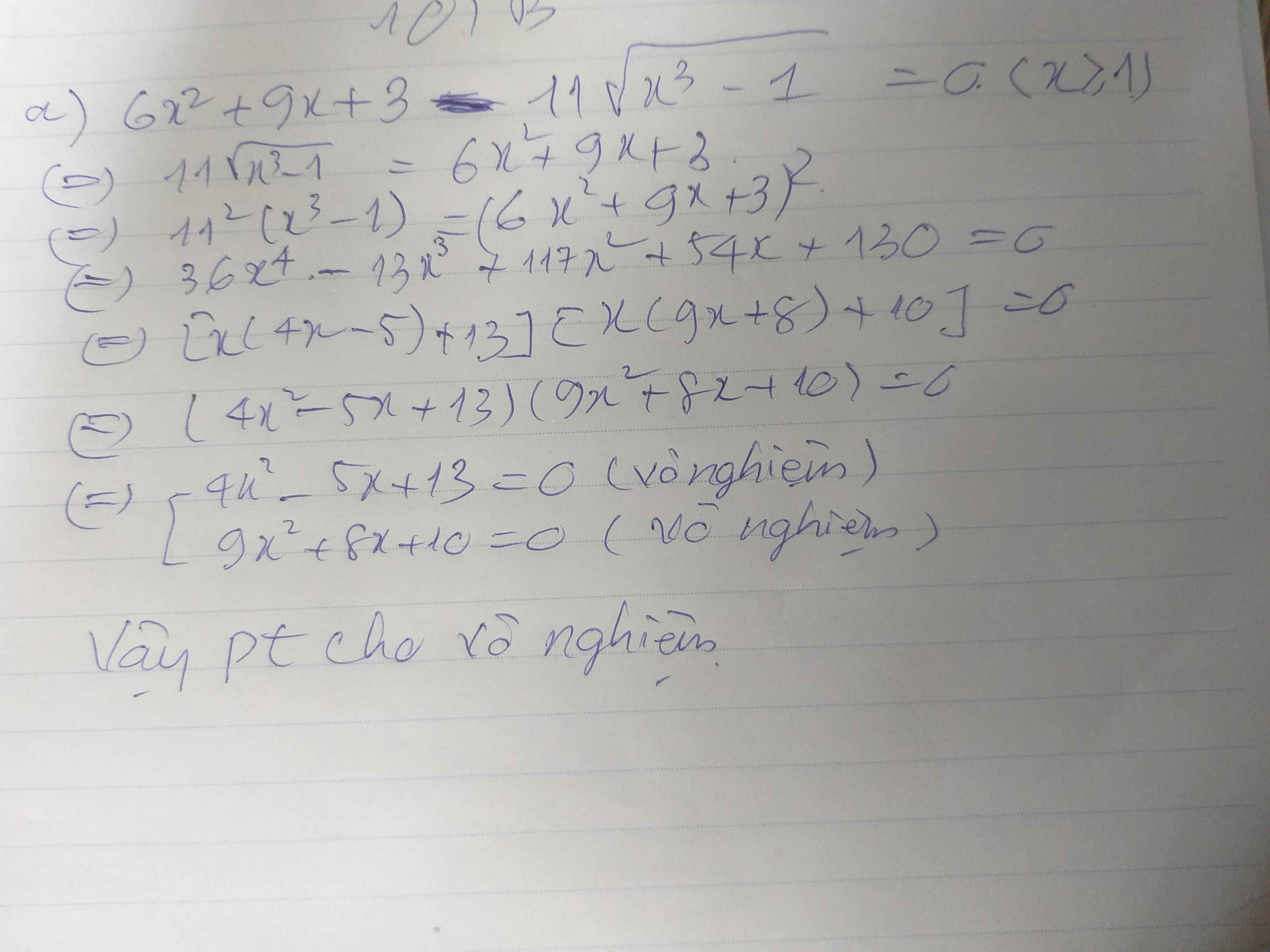
, mình đang cần giải gấp. Cảm ơn mn nhiều.
