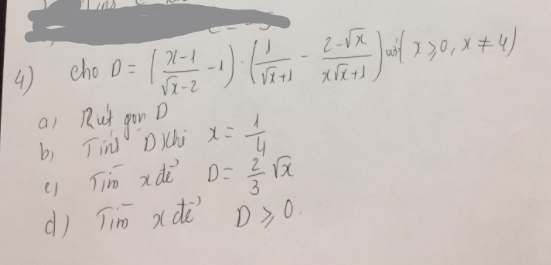Question

Mình cần từ bài 4 nhoa

Answer 1

Đăng tách ra đi bạn ơi. 1 bài mà nhiều như thế thì 1 lần 1 bài thoi

Answer 2

\(4,\\ a,P=\dfrac{x+\sqrt{x}+\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}:\dfrac{2\sqrt{x}+2-2+x}{x\left(\sqrt{x}+1\right)}\\ P=\dfrac{x+2\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{x\left(\sqrt{x}+1\right)}{x+2\sqrt{x}}=\dfrac{x}{\sqrt{x}-1}\\ b,P>2\Leftrightarrow\dfrac{x}{\sqrt{x}-1}-2>0\\ \Leftrightarrow\dfrac{x-2\sqrt{x}+2}{\sqrt{x}-1}>0\\ \Leftrightarrow\sqrt{x}-1>0\left(x-2\sqrt{x}+2=\left(\sqrt{x}-1\right)^2+1>0\right)\\ \Leftrightarrow x>1\\ c,P=\left|4\sqrt{x}-3\right|:\left(\sqrt{x}-1\right)\\ \Leftrightarrow\dfrac{x}{\sqrt{x}-1}=\dfrac{\left|4\sqrt{x}-3\right|}{\sqrt{x}-1}\Leftrightarrow\left|4\sqrt{x}-3\right|=x\\ \Leftrightarrow\left[{}\begin{matrix}4\sqrt{x}-3=x\left(x\ge\dfrac{9}{16}\right)\\3-4\sqrt{x}=x\left(x< \dfrac{9}{16}\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}x=9\left(tm\right)\\x=1\left(tm\right)\end{matrix}\right.\\\left[{}\begin{matrix}x=-2+\sqrt{7}\left(ktm\right)\\x=-2-\sqrt{7}\left(tm\right)\end{matrix}\right.\end{matrix}\right.\\ \Leftrightarrow x\in\left\{1;9;-2-\sqrt{7}\right\}\)

Answer 3

Bài 5:

b: Xét ΔAHB vuông tại H có HM là đường cao ứng với cạnh huyền AB

nên \(AM\cdot AB=AH^2\left(1\right)\)

Xét ΔAHC vuông tại H có HN là đường cao ứng với cạnh huyền AC

nên \(AN\cdot AC=AH^2\left(2\right)\)

Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)

hay \(\dfrac{AM}{AN}=\dfrac{AC}{AB}\)