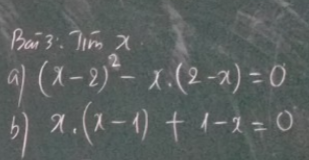`a)(x-2)^2-x(2-x)=0`
`<=>(x-2)^2+x(x-2)=0`
`<=>(x-2)(x-2+x)=0`
`<=>(x-2)(2x-2)=0`
`<=>(x-2)(x-1)=0`
`<=>x=2` hoặc `x=1`
Vậy `S={1;2}`
____________________________________
`b)x(x-1)+1-x=0`
`<=>x(x-1)-(x-1)=0`
`<=>(x-1)(x-1)=0`
`<=>(x-1)^2=0`
`<=>x-1=0`
`<=>x=1`
Vậy `S={1}`
\(a.\left(x-2\right)^2-x\left(2-x\right)=0\)
\(\Leftrightarrow\left(x-2\right)^2+x\left(x-2\right)=0\)
\(\Leftrightarrow\left(2x-2\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-2=0\\x-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
\(b.x\left(x-1\right)+1-x=0\)
\(\Leftrightarrow x\left(x-1\right)-\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)^2=0\)
\(\Leftrightarrow x-1=0\)
\(\Leftrightarrow x=1\)