\(A=x^2-x+\dfrac{9}{2x}+4=x^2-3x+\dfrac{9}{4}+2x+\dfrac{9}{2x}+\dfrac{7}{4}\)
\(=\left(x-\dfrac{3}{2}\right)^2+2x+\dfrac{9}{2x}+\dfrac{7}{4}\)
Áp dụng AM-GM có: \(2x+\dfrac{9}{2x}\ge2\sqrt{2x.\dfrac{9}{2x}}=6\)
Có \(\left(x-\dfrac{3}{2}\right)^2\ge0\forall x\)
\(\Rightarrow\left(x-\dfrac{3}{2}\right)^2+2x+\dfrac{9}{2x}+\dfrac{7}{4}\ge0+6+\dfrac{7}{4}\Leftrightarrow A\ge\dfrac{31}{4}\)
Dấu "=" xảy ra khi \(x=\dfrac{3}{2}\)
Vậy \(A_{min}=\dfrac{31}{4}\) tại \(x=\dfrac{3}{2}\)
\(A=x^2-3x+\dfrac{9}{4}+2\left(x-3+\dfrac{9}{4x}\right)+\dfrac{31}{4}\)
\(A=\left(x-\dfrac{3}{2}\right)^2+2\left(\sqrt{x}-\dfrac{3}{2\sqrt{x}}\right)^2+\dfrac{31}{4}\ge\dfrac{31}{4}\)
\(A_{min}=\dfrac{31}{4}\) khi \(x=\dfrac{3}{2}\)











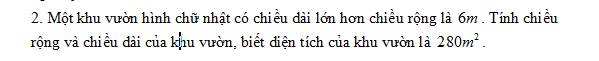












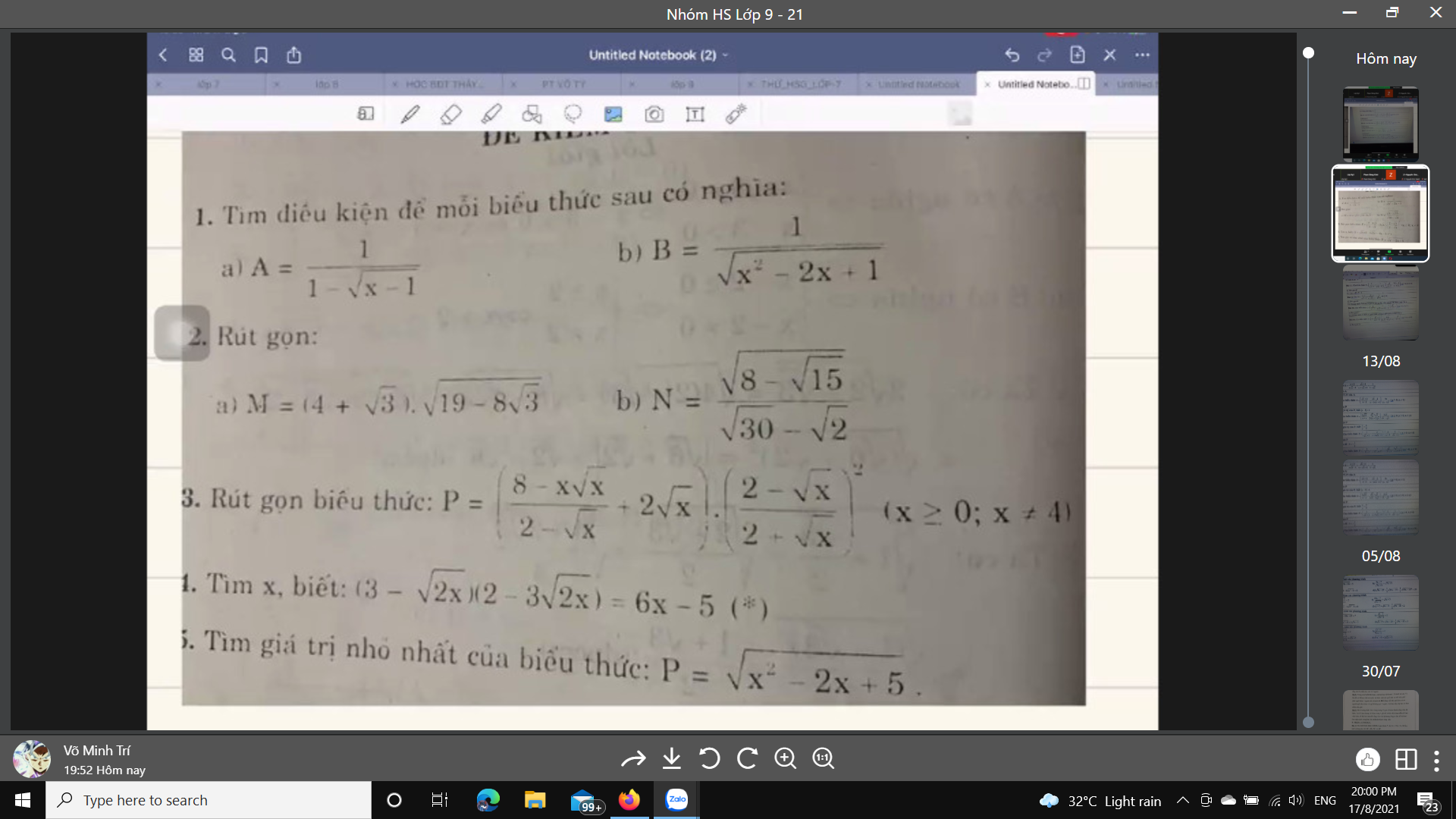 làm nhanh giúp mình ạ
làm nhanh giúp mình ạ
 mong mọi người làm nhanh giúp mình
mong mọi người làm nhanh giúp mình