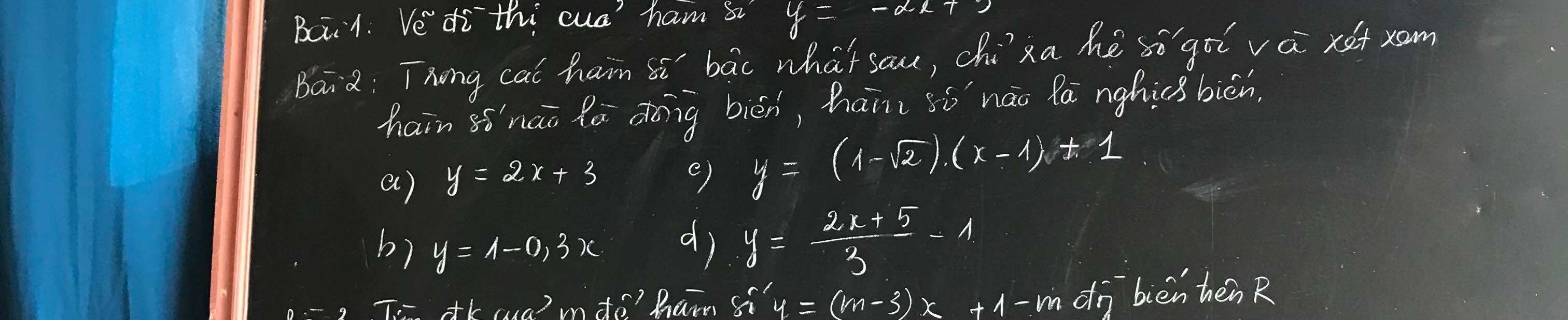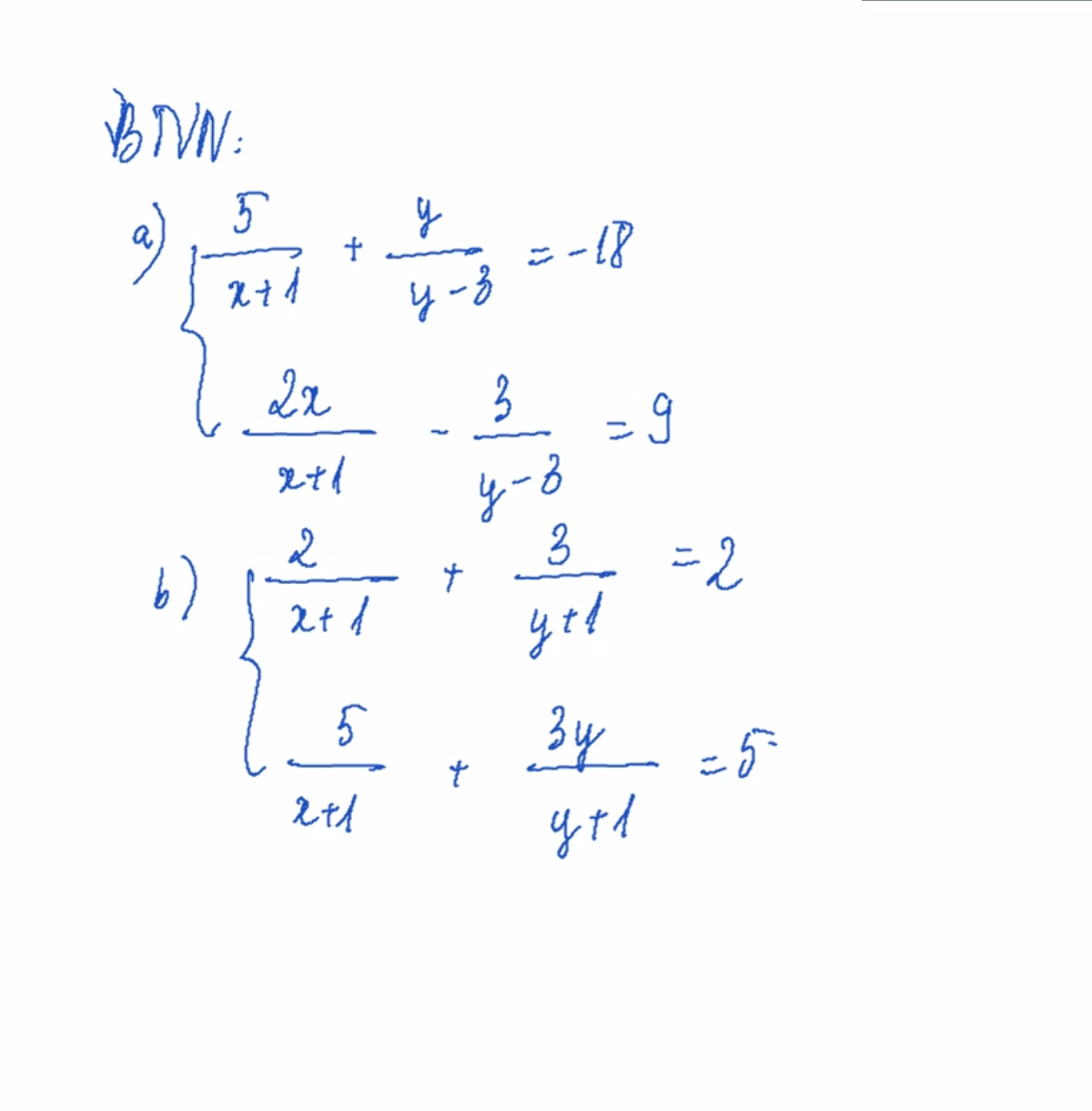\(\left(d\right):y=\left(m+2\right)x+2m-1\)
\(\left(d'\right):y=-2x+1\)
a) \(A\left(-1;-2\right)\in\left(d\right)\Leftrightarrow\left(m+2\right).\left(-2\right)+2m-1=-2\)
\(\Leftrightarrow-2m=3\)
\(\Leftrightarrow m=-\dfrac{3m}{2}\)
b) \(\left(d\right)//\left(d'\right)\Leftrightarrow\left\{{}\begin{matrix}m+2=-2\\2m-1\ne1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m=-4\\m\ne1\end{matrix}\right.\) \(\Leftrightarrow m=4\)
c) \(\left(d\right)\perp\left(d'\right)\Leftrightarrow\left(m+2\right).\left(-2\right)=-1\Leftrightarrow2m=-3\Leftrightarrow m=-\dfrac{3}{2}\)
d) Giả sử điểm \(\text{M(x₀, y₀)}\) là điểm cố định mà đường thẳng \(\text{(d)}\) luôn đi qua. Khi đó, với mọi giá trị của \(\text{m}\), ta có:
\(y_o=\left(m+2\right)x_o+2m-1\)
\(\Leftrightarrow y_o=mx_o+2x_o+2m-1\)
\(\Leftrightarrow m\left(x_o+2\right)+\left(2x_o-y_o-1\right)=0\)
Để phương trình trên đúng \(\forall m\), ta phải có:
\(\left\{{}\begin{matrix}x_o+2=0\\2x_o-y_o-1=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x_o=-2\\y_o=-5\end{matrix}\right.\)
Vậy, với mọi giá trị của \(\text{m}\), đường thẳng \(\text{(d)}\) luôn đi qua điểm cố định \(\text{M(-2;-5).}\)
g: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\\left(m+2\right)x+2m-1=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\x=\dfrac{-2m+1}{m+2}\end{matrix}\right.\)
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=\left(m+2\right)x+2m-1=2m-1\end{matrix}\right.\)
\(OA=\sqrt{\left(\dfrac{-2m+1}{m+2}-0\right)^2+\left(0-0\right)^2}=\sqrt{\left(\dfrac{-2m+1}{m+2}\right)^2}=\left|\dfrac{2m-1}{m+2}\right|\)
\(OB=\sqrt{\left(0-0\right)^2+\left(2m-1-0\right)^2}=\sqrt{\left(2m-1\right)^2}=\left|2m-1\right|\)
ΔOAB vuông tại O
=>\(S_{OAB}=\dfrac{1}{2}\cdot OA\cdot OB\)
\(=\dfrac{1}{2}\cdot\left|2m-1\right|\cdot\dfrac{\left|2m-1\right|}{\left|m+2\right|}=\dfrac{\dfrac{1}{2}\left(2m-1\right)^2}{\left|m+2\right|}\)
\(S_{AOB}=1\)
=>\(\dfrac{1}{2}\cdot\dfrac{\left(2m-1\right)^2}{\left|m+2\right|}=1\)
=>\(\dfrac{\left(2m-1\right)^2}{\left|m+2\right|}=2\)
=>\(\left(2m-1\right)^2=2\cdot\left|m+2\right|\left(1\right)\)
TH1: m>-2
(1) sẽ trở thành:
\(\left(2m-1\right)^2=2\left(m+2\right)\)
=>\(4m^2-4m+1-2m-4=0\)
=>\(4m^2-6m-3=0\)
=>\(\left[{}\begin{matrix}m=\dfrac{3+\sqrt{21}}{4}\left(nhận\right)\\m=\dfrac{3-\sqrt{21}}{4}\left(nhận\right)\end{matrix}\right.\)
TH2: m<-2
(1) sẽ trở thành:
\(\left(2m-1\right)^2=-2\left(m+2\right)\)
=>\(4m^2-4m+1+2m+4=0\)
=>\(4m^2-2m+5=0\)
\(\text{Δ}=\left(-2\right)^2-4\cdot4\cdot5=4-16\cdot5=4-80=-76< 0\)
=>Phương trình vô nghiệm


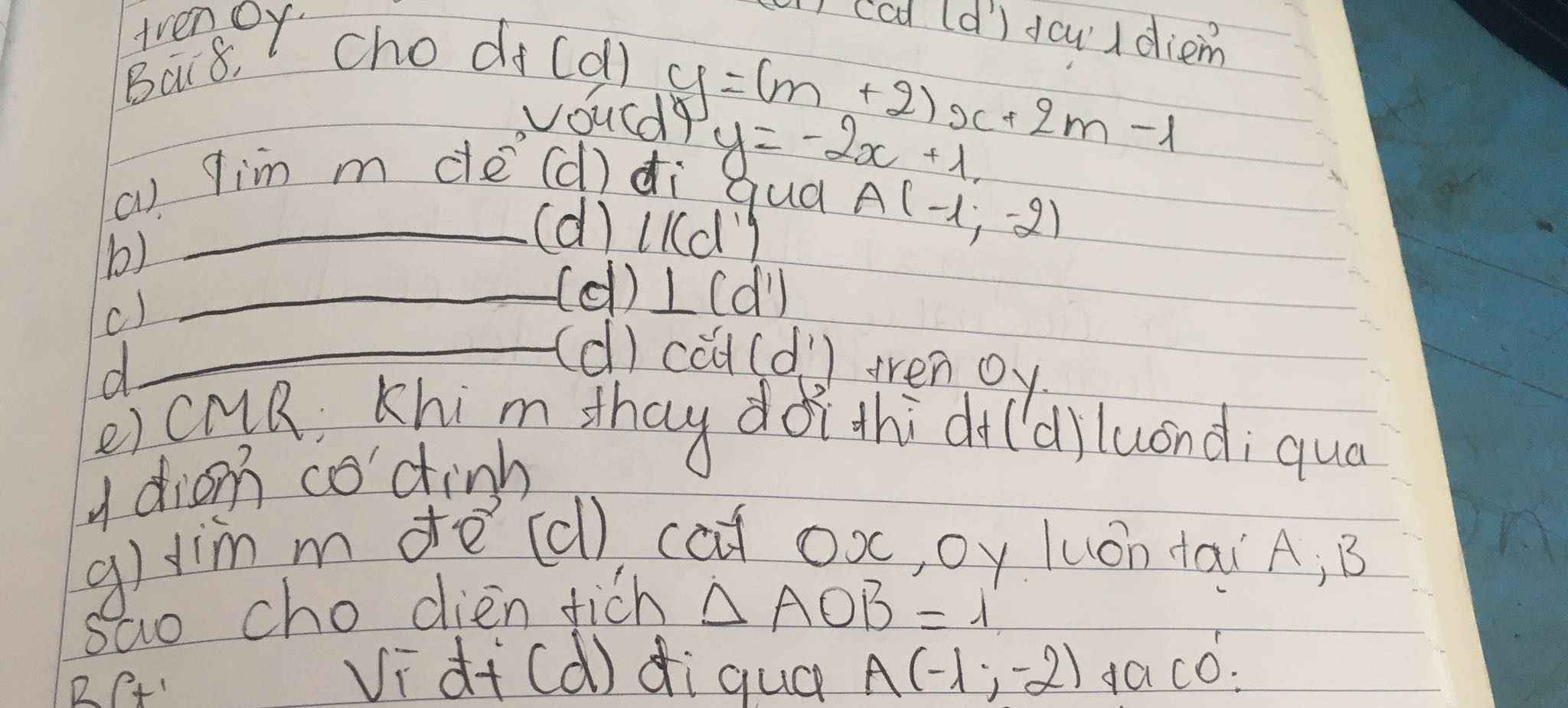







 giải hộ mk vs chỉ cần có cách làm câu b thôi câu a thì ko cần
giải hộ mk vs chỉ cần có cách làm câu b thôi câu a thì ko cần