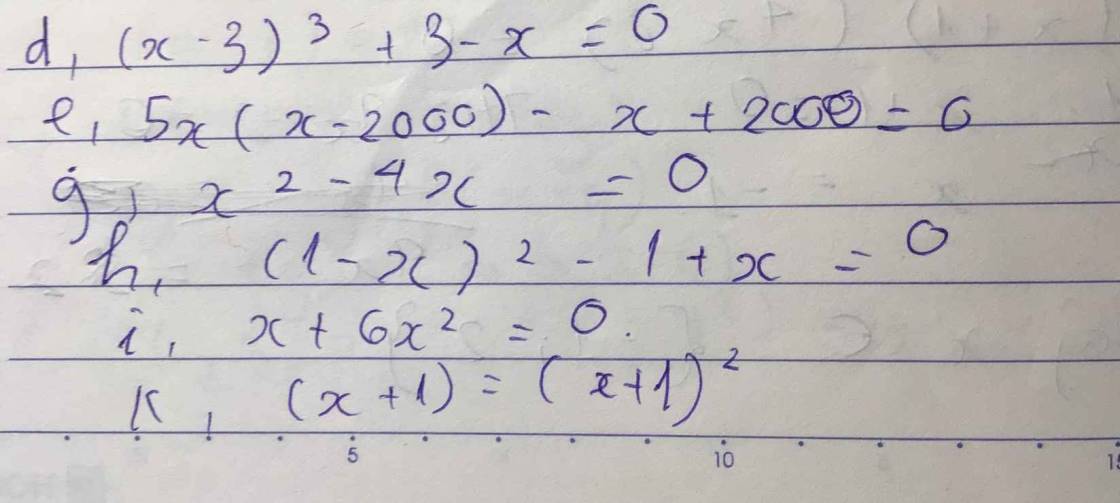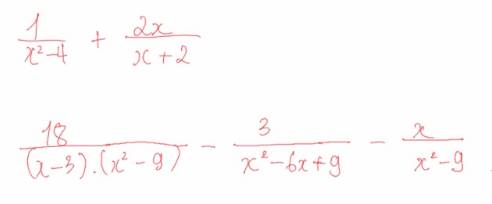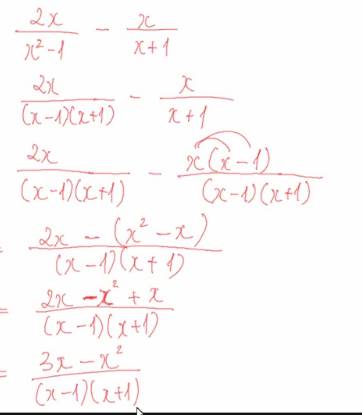Bài 2:
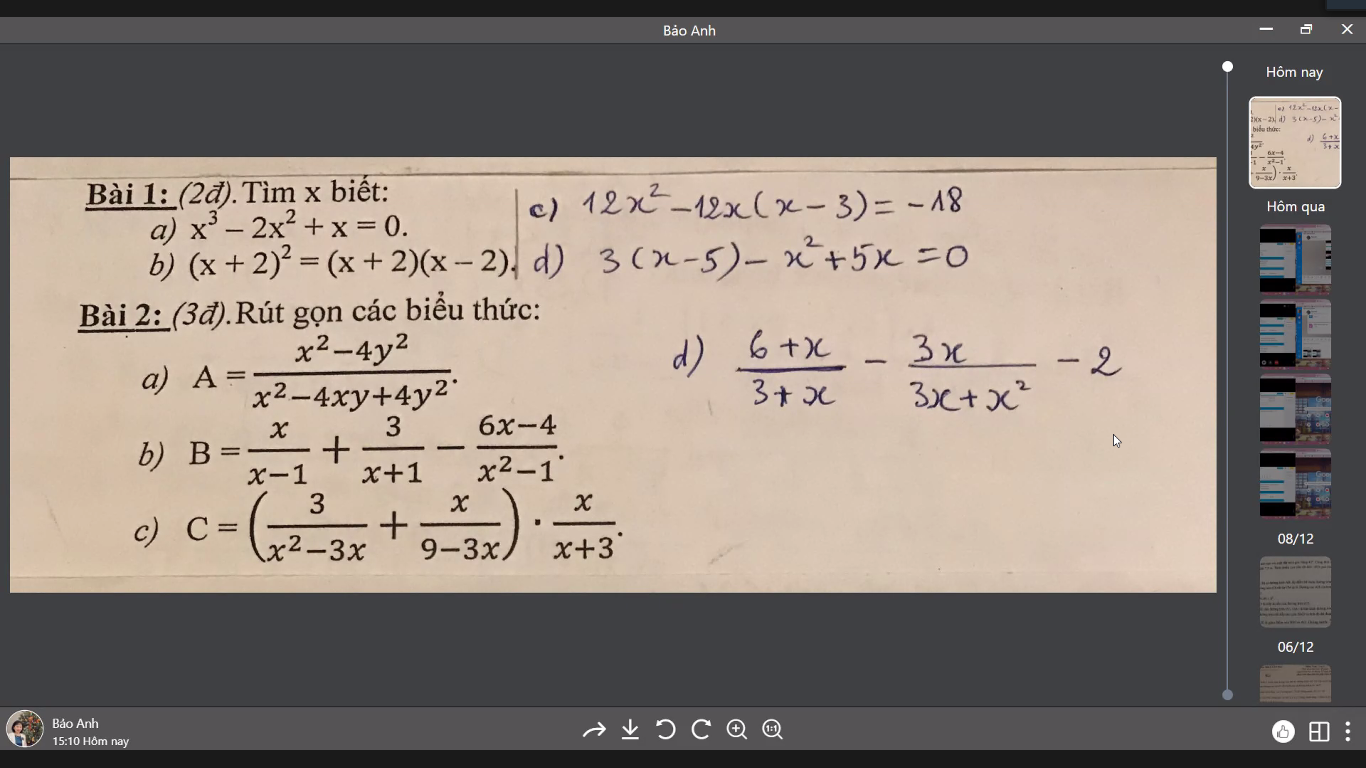
\(a,\dfrac{x^2-4y^2}{x^2-4xy+4y^2}=\dfrac{\left(x-2y\right)\left(x+2y\right)}{\left(x-2y\right)^2}=\dfrac{x+2y}{x-2y}\)
\(b,\dfrac{x}{x-1}+\dfrac{3}{x+1}-\dfrac{6x-4}{x^2-1}=\dfrac{x\left(x+1\right)+3\left(x-1\right)-\left(6x-4\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{x^2+x+3x-3-6x+4}{\left(x-1\right)\left(x+1\right)}=\dfrac{x^2-2x+1}{\left(x-1\right)\left(x+1\right)}=\dfrac{\left(x-1\right)^2}{\left(x-1\right)\left(x+1\right)}=\dfrac{x-1}{x+1}\)
\(c,\left(\dfrac{3}{x^2-3x}+\dfrac{x}{9-3x}\right).\dfrac{x}{x+3}=\left(\dfrac{3}{x\left(x-3\right)}-\dfrac{x}{3\left(x-3\right)}\right).\dfrac{x}{x+3}=\dfrac{9-x^2}{x\left(x-3\right)}.\dfrac{x}{x+3}=\dfrac{\left(3-x\right)\left(3+x\right)}{-x\left(3-x\right)}.\dfrac{x}{x+3}=-1\)
\(d,\dfrac{6+x}{3+x}-\dfrac{3x}{3x+x^2}-2=\dfrac{6+x}{3+x}-\dfrac{3}{3+x}-2=\dfrac{6+x-3}{3+x}-2=\dfrac{3+x}{3+x}-2=1-2=-1\)
Bài 1
\(x^3-2x^2+x=0\\ \Leftrightarrow x\left(x^2-2x+1\right)=0\\ \Leftrightarrow x\left(x-1\right)^2=0\)
\(\Leftrightarrow x=0\) hoặc \(\left(x-1\right)^2=0\\ \Leftrightarrow x-1=0\\ \Leftrightarrow x=1\)
\(\left(x+2\right)^2=\left(x+2\right)\left(x-2\right)\\ \Leftrightarrow\left(x+2\right)^2-\left(x+2\right)\left(x-2\right)=0\\ \Leftrightarrow\left(x+2\right)\left(x+2-x+2\right)=0\)
\(\Leftrightarrow\left(x+2\right)4=0\\ \Leftrightarrow4x+8=0\\ \Leftrightarrow4x=-8\\ \Leftrightarrow x=-\dfrac{8}{4}\\ \Leftrightarrow x=-2\)
d. 3(x - 5) - x(x - 5)
⇔ (x - 5)(3 - x)
⇔ x - 5 = 0 hoặc 3 - x = 0
⇔ x =5 - x = - 3
⇔ x =5 x = 3