Question

làm hết nhé ạ!

Answer 1

Bài 3:

1: ĐKXĐ: x<>-y/2

\(\left\{{}\begin{matrix}\dfrac{4x-y}{2x+y}-\dfrac{x-2y}{2x+y}=2\\3x-y=4\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}\dfrac{4x-y-x+2y}{2x+y}=2\\3x-y=4\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}3x-y=2\left(2x+y\right)\\3x-y=4\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}3x-y-4x-2y=0\\3x-y=4\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}-x-3y=0\\3x-y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3x-9y=0\\3x-y=4\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}-10y=4\\3x-y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-\dfrac{2}{5}\\3x=y+4=-\dfrac{2}{5}+4=\dfrac{18}{5}\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=-\dfrac{2}{5}\\x=\dfrac{6}{5}\end{matrix}\right.\left(nhận\right)\)

2: 

a: Thay x=1 và y=2 vào (d_m), ta được:

\(1\left(2m-1\right)-m+1=2\)

=>2m-1-m+1=2

=>m=2

Thay m=2 vào (d_m), ta được:

\(y=\left(2\cdot2-1\right)x-2+1=3x-1\)

Vẽ đồ thị:

 

 

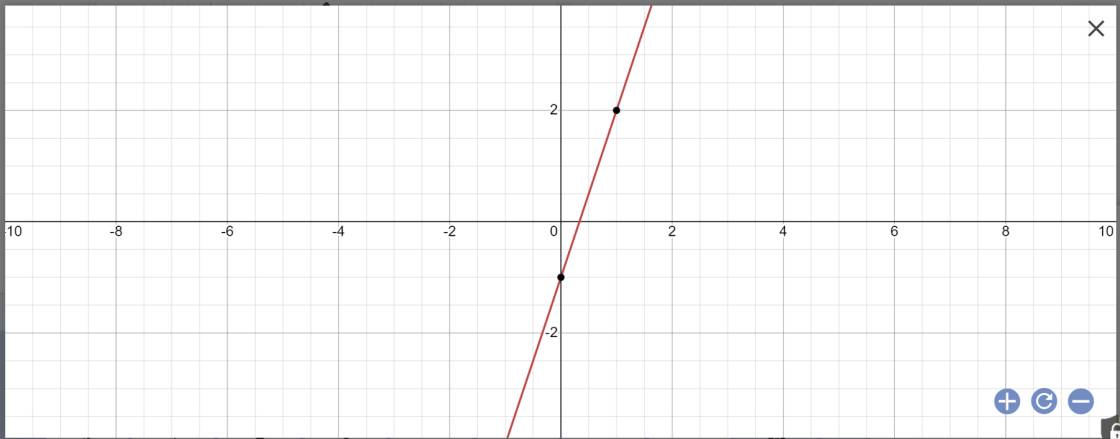
b: tọa độ giao điểm của (d_m) với trục hoành là:

\(\left\{{}\begin{matrix}y=0\\\left(2m-1\right)x-m+1=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=0\\x\left(2m-1\right)=m-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=\dfrac{m-1}{2m-1}\end{matrix}\right.\)

Để x nguyên thì \(m-1⋮2m-1\)

=>\(2m-2⋮2m-1\)

=>\(2m-1-1⋮2m-1\)

=>\(-1⋮2m-1\)

=>\(2m-1\in\left\{1;-1\right\}\)

=>\(2m\in\left\{2;0\right\}\)

=>\(m\in\left\{1;0\right\}\)