5.
$|E|=|x_1-x_2|=\sqrt{(x_1-x_2)^2}=\sqrt{(x_1+x_2)^2-4x_1x_2}$
$\Rightarrow E=\pm \sqrt{(x_1+x_2)^2-4x_1x_2}$
6.
$|F|=|x_1^2-x_2^2|=|x_1-x_2|.|x_1+x_2|=\sqrt{(x_1+x_2)^2-4x_1x_2}.|x_1+x_2|$
$\Rightarrow F=\pm \sqrt{(x_1+x_2)^2-4x_1x_2}(x_1+x_2)$
7.
$G=x_1^3-x_2^3=(x_1-x_2)(x_1^2+x_1x_2+x_2^2)$
$=(x_1-x_2)[(x_1+x_2)^2-x_1x_2]=E[(x_1+x_2)^2-x_1x_2]$
8.
$H=x_1^4+x_2^4=(x_1^2+x_2^2)(x_1^2-x_2^2)=AF$
9.
$I=\frac{1}{x_1}+\frac{1}{x_2}=\frac{x_1+x_2}{x_1x_2}$10.
$K=\frac{1}{x_1-1}+\frac{1}{x_2-1}=\frac{x_2-1+x_1-1}{(x_1-1)(x_2-1)}=\frac{(x_1+x_2)-2}{x_1x_2-(x_1+x_2)+1}$
11.
$L=\frac{x_2}{x_1-1}+\frac{x_1}{x_2-1}=\frac{x_2^2-x_2+x_1^2-x_1}{(x_1-1)(x_2-1)}$
$=\frac{(x_1^2+x_2^2)-(x_1+x_2)}{(x_1-1)(x_2-1)}$
$=\frac{A-(x_1+x_2)}{x_1x_2-(x_1+x_2)+1}$
12.
M=\frac{1}{x_1}-\frac{1}{x_2}=\frac{x_2-x_1}{x_1x_2}=\frac{-E}{x_1x_2}$
13.
$N=|x_1-x_2|=\sqrt{(x_1-x_2)^2}=\sqrt{(x_1+x_2)^2-4x_1x_2}$
14.
$P=|x_1|+|x_2|=\sqrt{(|x_1|+|x_2|)^2}=\sqrt{x_1^2+x_2^2+2|x_1x_2|}$
$=\sqrt{(x_1+x_2)^2-2x_1x_2+2|x_1x_2|}$
15.
$Q=\sqrt{x_1}+\sqrt{x_2}=\sqrt{(\sqrt{x_1}+\sqrt{x_2})^2}=\sqrt{x_1+x_2+2\sqrt{x_1x_2}}$
16.
$T=x_1\sqrt{x_1}+x_2\sqrt{x_2}$
$=\sqrt{x_1x_2}(\sqrt{x_1}+\sqrt{x_2})=\sqrt{x_1x_2}.Q$
1.
$A=x_1^2+x_2^2=(x_1+x_2)^2-2x_1x_2$
2.
$x_1^2-x_2^2=(x_1-x_2)(x_1+x_2)$. Trong đó:
$x_1-x_2=\pm \sqrt{(x_1+x_2)^2-4x_1x_2}$
3.
$x_1^3+x_2^3=(x_1+x_2)^3-3x_1x_2(x_1+x_2)$
4.
$x_1^4+x_2^4=(x_1^2+x_2)^2-2(x_1x_2)^2=[(x_1+x_2)^2-2x_1x_2]^2-2(x_1x_2)^2$








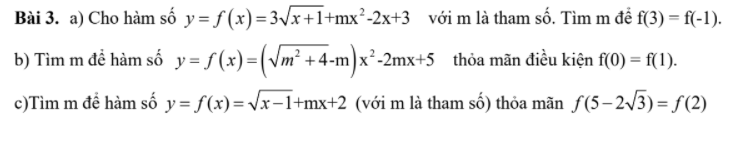




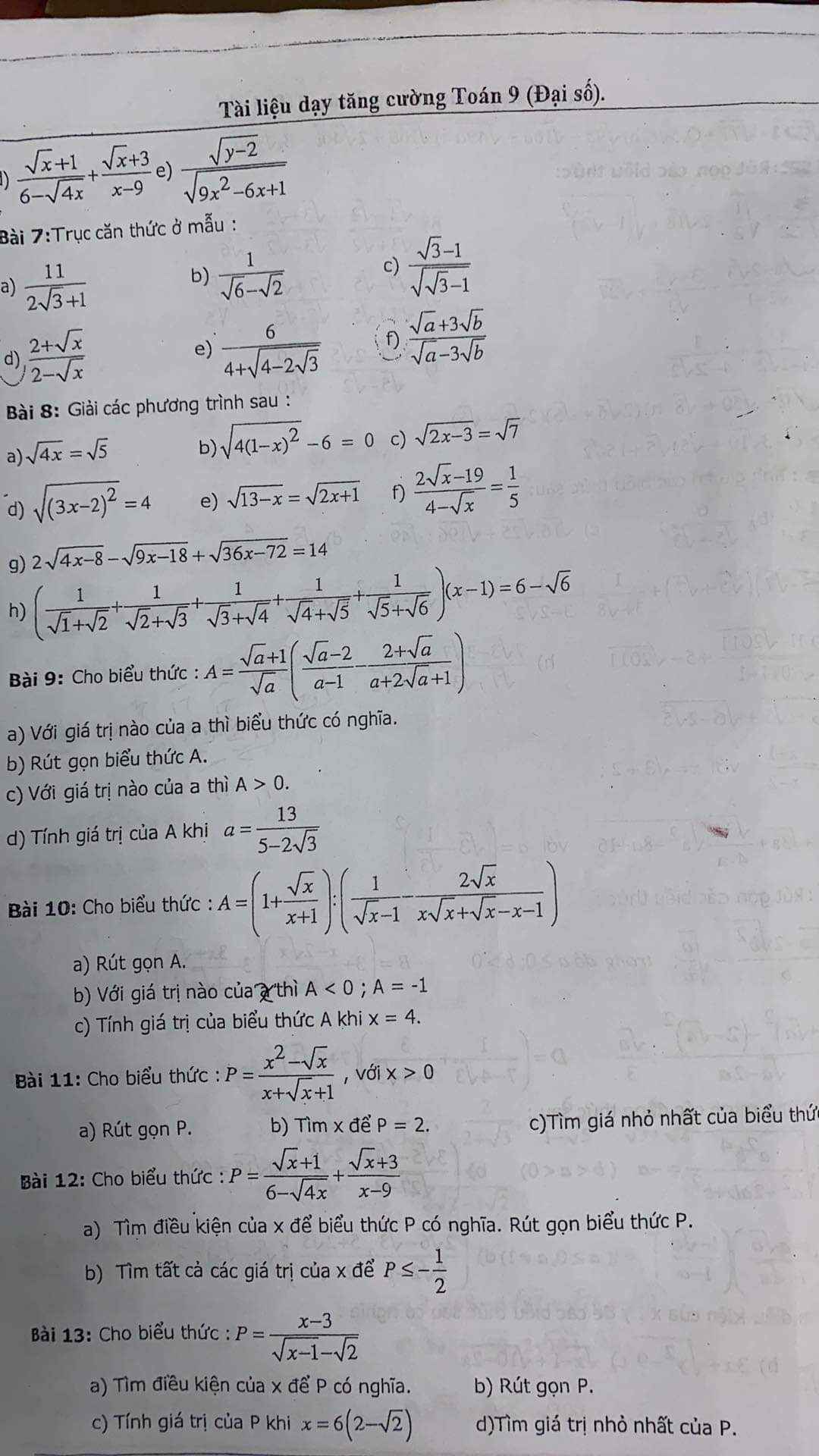
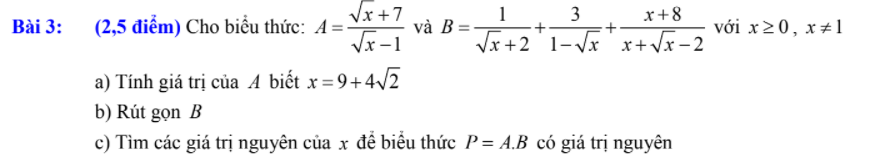 được không ạ, mai em phải nộp rồi, cảm ơn mn nhiều.
được không ạ, mai em phải nộp rồi, cảm ơn mn nhiều. 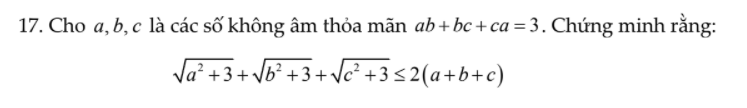 câu này với ạ! Mình cảm ơn.
câu này với ạ! Mình cảm ơn.