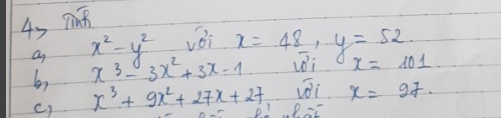Bài 16
a) x² + 2x + 2
= x² + 2x + 1 + 1
= (x + 1)² + 1
Do (x + 1)² ≥ 0 với mọi x ∈ R
⇒ (x + 1)² + 1 > 0 với mọi x ∈ R
b) 9a² - 6a + 3
= 9a² - 6a + 1 + 2
= (3a - 1)² + 2
Do (3a - 1)² ≥ 0 với mọi a ∈ R
⇒ (3a - 1)² + 2 > 0 với mọi a ∈ R
Bài 17
M = y² + 6y + 7
= y² + 6y + 9 - 2
= (y + 3)² - 2
(y + 3)² ≥ 0 với mọi y ∈ R
⇒ (y + 3)² - 2 ≥ -2 với mọi y ∈ R
Vậy GTNN của M là -2 khi y = -3
------------
H = 16b² - 16b + 5
= 16b² - 16 + 4 + 1
= (4b - 2)² + 1
Do (4b - 2)² ≥ 0 với mọi b ∈ R
⇒ (4b - 2)² + 1 ≥ 1 với mọi b ∈ R
Vậy GTNN của H là 1 khi b = 1/2
------------
T = x² + y² + 2x + 1 - 2y
= x² + 2x + 1 + y² - 2y + 1 - 1
= (x + 1)² + (y - 1)² - 1
Do (x + 1)² ≥ 0 với mọi x ∈ R
(y - 1)² ≥ 0 với mọi y ∈ R
⇒ (x + 1)² + (y - 1)² ≥ 0 với mọi x, y ∈ R
⇒ (x + 1)² + (y - 1)² - 1 ≥ -1 với mọi x, y ∈ R
Vậy GTNN của T là -1 khi x = -1; y = 1
Bài 18
a) -x² + 6x - 12
= -(x² - 6x + 12)
= -(x² - 6x + 9 + 3)
= -(x - 3)² - 3
Do (x - 3)² ≥ 0 với mọi x ∈ R
⇒ -(x - 3)² ≤ 0 với mọi x ∈ R
⇒ -(x - 3)² - 3 < 0 với mọi x ∈ R
b) -9y² + 6y - 3
= -(9y² - 6y + 3)
= -(9y² - 6y + 1 + 2)
= -(3y - 1)² - 2
Do (3y - 1)² ≥ 0 với mọi y ∈ R
⇒ -(3y - 1)² ≤ 0 với mọi y ∈ R
⇒ -(3y - 1)² - 2 < 0 với mọi y ∈ R






 giải giúp bài 10 ạ
giải giúp bài 10 ạ
 giúp mình bài 4 câu B,C D với ạ
giúp mình bài 4 câu B,C D với ạ