Bài 7
Ta có:
VT = a³ + b³ = (a + b)(a² - ab + b²)
= (a + b)(a² - 2ab + b² + ab)
= (a + b)[(a - b)² + ab]
= VP
Vậy a³ + b³ = (a + b)[(a - b)² + ab]
Bài 8
(x + 2)³ + (x - 2)³ + x³ - 3x(x + 2)(x - 2)
= x³ + 6x² + 12x + 8 + x³ - 6x² + 12x - 8 + x³ - 3x(x² - 4)
= 3x³ + 24x - 3x³ + 12x
= 36x
Bài 9
Ta có:
VT = (x + y)³ - (x - y)³
= x³ + 3x²y + 3xy² + y³ - x³ + 3x²y - 3xy² + y³
= 6x²y + 2y³
= 2y(3x² + y²)
= VP
Vậy (x + 2)³ - (x - y)³ = 2y(3x² + y²)
Bài 7 :
\(VP=\left(a+b\right)\left[\left(a-b\right)^2+ab\right]\)
\(=\left(a+b\right)\left(a^2-2ab+b^2+ab\right)\)
\(=\left(a+b\right)\left(a^2+b^2-ab\right)\)
\(=a^3+ab^2-a^2b+a^2b+b^3-ab^2\)
\(=a^3+b^3=VT\left(dpcm\right)\)
Bài 8 :
\(\left(x+2\right)^3+\left(x-2\right)^3+x^3-3x\left(x-2\right)\left(x+2\right)\)
\(=x^3+6x^2+12x+8+x^3-6x^2+12x-8+x^3-3x\left(x^2-4\right)\)
\(=3x^3+24x-3x^3+12x\)
\(=36x\)
Bài 9 :
\(VT=\left(x+y\right)^3-\left(x-y\right)^3\)
\(=x^3+3xy^2+3x^2y+y^3-x^3+3x^2y-3xy^2+y^3\)
\(=6x^2y+2y^3\)
\(VP=2y\left(3x^2+y^2\right)=6x^2y+2y^3\)
\(\Rightarrow VT=VP\left(dpcm\right)\)
Bài 10
M = 2(x³ - y³) - 3(x² + y²)
= 2(x - y)(x² + xy + y²) - 3(x² + y²)
= 2x² + 2xy + 2y² - 3x² - 3y²
= -x² + 2xy - y²
= -(x² - 2xy + y²)
= -(x - y)²
= -1²
= -1










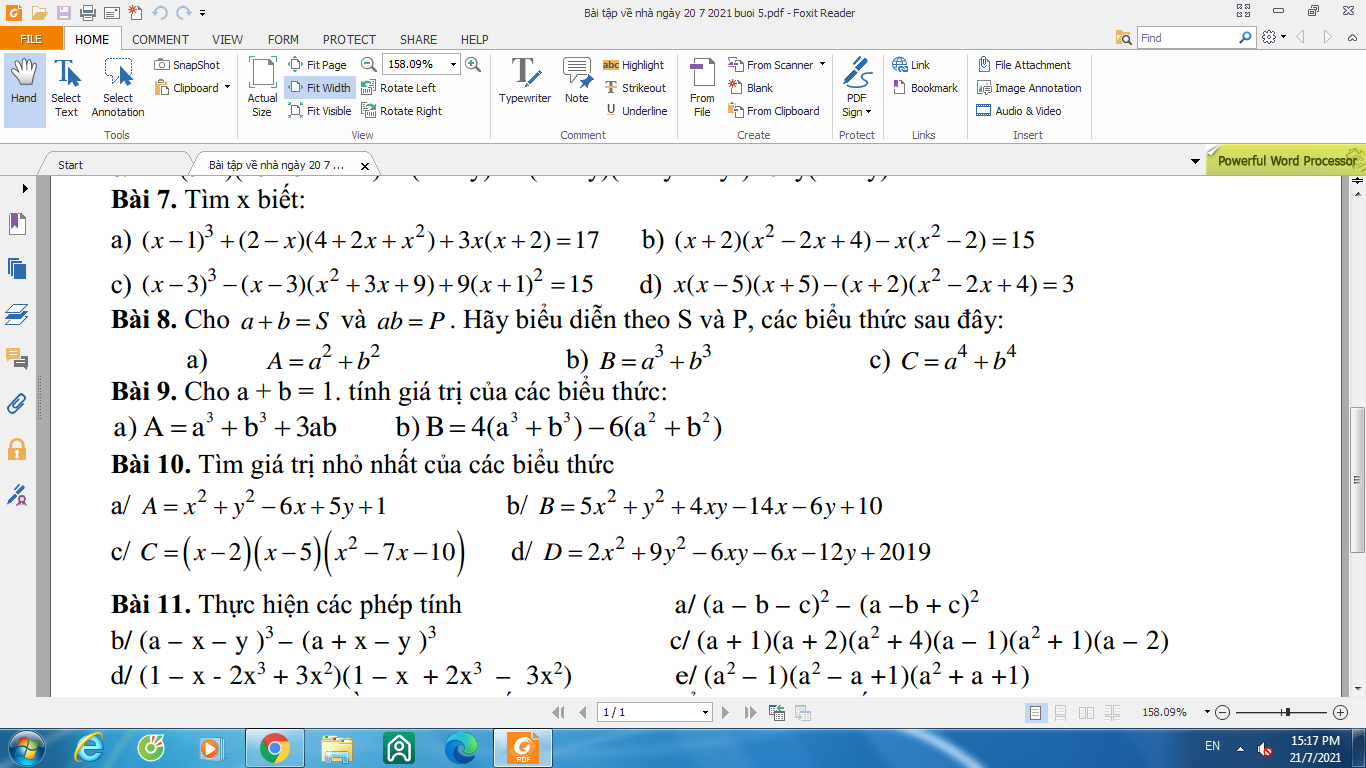





 giải giúp bài 10 ạ
giải giúp bài 10 ạ

