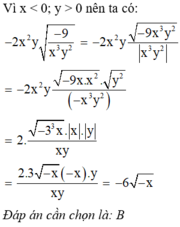Các câu hỏi tương tự
Khử mẫu biểu thức sau -xy 3 xy với x < 0; y < 0 ta được:
A. xy
B. - xy
C. 3 xy
D. - 3 xy
Khử mẫu biểu thức sau xy
4
x
2
y
2
với x 0; y 0 ta được: A. 4 B.
-
xy
C.
2
D. 2
Đọc tiếp
Khử mẫu biểu thức sau xy 4 x 2 y 2 với x > 0; y > 0 ta được:
A. 4
B. - xy
C. 2
D. 2
Rút gọn biểu thức sau
a/ A=\(\frac{x\sqrt{y}-y\sqrt{x}}{\sqrt{xy}}+\frac{x-y}{\sqrt{x}-\sqrt{y}}\)Với x>0 ; y>0 ;x#y
b/ B=\(\frac{3}{2+\sqrt{3}}+\frac{13}{4-\sqrt{3}}+\frac{6}{\sqrt{3}}\)
c/ C=\(\frac{\sqrt{4-2\sqrt{3}}}{\sqrt{6}-\sqrt{2}}\)
d/ D=\(\left(3\sqrt{2}+\sqrt{6}\right)\sqrt{6-3\sqrt{3}}\)
Rút gọn các biểu thức sau:a,Afrac{3}{2+sqrt{3}}+frac{13}{4-sqrt{3}}+frac{6}{sqrt{3}}b,Bfrac{xsqrt{y-ysqrt{x}}}{sqrt{xy}}+frac{x-y}{sqrt{x-sqrt{y}}} với x0 ;y0;xne yc,Cfrac{sqrt{4-2sqrt{3}}}{sqrt{6-sqrt{2}}}d,Dleft(3sqrt{2+sqrt{6}}right)sqrt{6-3sqrt{3}}
Đọc tiếp
Rút gọn các biểu thức sau:
a,A=\(\frac{3}{2+\sqrt{3}}\)+\(\frac{13}{4-\sqrt{3}}\)+\(\frac{6}{\sqrt{3}}\)
b,B=\(\frac{x\sqrt{y-y\sqrt{x}}}{\sqrt{xy}}\)+\(\frac{x-y}{\sqrt{x-\sqrt{y}}}\) với x>0 ;y>0;\(x\ne y\)
c,C=\(\frac{\sqrt{4-2\sqrt{3}}}{\sqrt{6-\sqrt{2}}}\)
d,D=\(\left(3\sqrt{2+\sqrt{6}}\right)\)\(\sqrt{6-3\sqrt{3}}\)
với x>y≥0, biểu thức:\(\dfrac{1}{y-x}\sqrt{x^6\left(x-y\right)2}\)rút gọn bt ta đc...
1) Với giá trị nào của x ta có \(x\sqrt{3}=-\sqrt{3x^2}\)
2) Đưa thừa số vào trong dấu căn của biểu thức \(ab^2\sqrt{a}\) với a > 0 ta được :
3) Khử mẫu của biểu thức \(a\sqrt{\dfrac{b}{a}}\) (với a>0) ta được :
Rút gọn biểu thức :a) sqrt{left(sqrt{x}-sqrt{y}right)^2left(sqrt{x}+sqrt{y}right)^2} với 0 lex leyb) frac{3-sqrt{x}}{x-9}(với x ge0 , x ne9)c) frac{x-5sqrt{x}+6}{sqrt{x}-3}( với xge0 , xne9)d) 6-2x-sqrt{9-6x+x^2}(với x 3)
Đọc tiếp
Rút gọn biểu thức :
a) \(\sqrt{\left(\sqrt{x}-\sqrt{y}\right)^2\left(\sqrt{x}+\sqrt{y}\right)^2}\) với 0 \(\le\)x \(\le\)y
b) \(\frac{3-\sqrt{x}}{x-9}\)(với x \(\ge\)0 , x \(\ne\)9)
c) \(\frac{x-5\sqrt{x}+6}{\sqrt{x}-3}\)( với x\(\ge\)0 , x\(\ne\)9)
d) \(6-2x-\sqrt{9-6x+x^2}\)(với x <3)
1. phân tích đa thức thành nhân tử
a)x^2-13
b)x+5√x +6(x≥0)
c)x-4√x +3(x≥0)
d) 3x-6√x -6(x≥0)
2 Tìm GTNN của:
a) A= x-√x +3
b) B=x+3√x +5
c) C=x^4-8xy-x^2y+x^2y^2-xy^2+y^4+2000
1, tính a/ (3+√5)(√10 - √2)√(3-√5)b/[√2-√(3-√5)].√2c/(√10 + √6).√(8-2√15)2, tìm x biết a/ √(x+5)1+√xb/√x + √(x-1)1c/ √(3-x) + √(x-5)103, phân tích đa thức thành nhân tử:a/ ab+b√a+√a+1 với a ≥0b/ x-2√xy + y với x,y ≥ 0c/√xy + 2√x - 3√y -6 với x,y ≥ 04, chứng minh rằng a/ (4+√15).(√10-√6).√(4-√15)2b/ √a + √b √(a+b) (a,b0)5, Cho √(8-a) + √(5+a) 5 tính √[(8-a).(5+a)]6, rút gọn √(7+2√10)-√15P/s : mn giúp e với nha
Đọc tiếp
1, tính a/ (3+√5)(√10 - √2)√(3-√5)
b/[√2-√(3-√5)].√2
c/(√10 + √6).√(8-2√15)
2, tìm x biết a/ √(x+5)=1+√x
b/√x + √(x-1)=1
c/ √(3-x) + √(x-5)=10
3, phân tích đa thức thành nhân tử:
a/ ab+b√a+√a+1 với a ≥0
b/ x-2√xy + y với x,y ≥ 0
c/√xy + 2√x - 3√y -6 với x,y ≥ 0
4, chứng minh rằng a/ (4+√15).(√10-√6).√(4-√15)=2
b/ √a + √b > √(a+b) (a,b>0)
5, Cho √(8-a) + √(5+a) = 5 tính √[(8-a).(5+a)]
6, rút gọn √(7+2√10)-√15
P/s : mn giúp e với nha