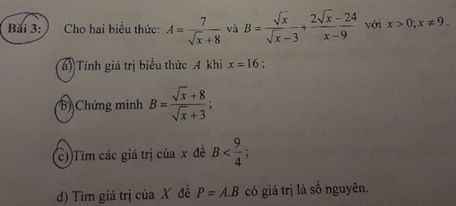2: \(\text{Δ}=\left(m-2\right)^2-4\cdot1\left(-8\right)=\left(m-2\right)^2+32>=32>0\forall m\)
=>Phương trình luôn có hai nghiệm phân biệt
Theo Vi-et, ta được:
\(x_1+x_2=-\dfrac{b}{a}=-m+2;x_1x_2=\dfrac{c}{a}=-8\)
\(Q=\left(x_1^2-4\right)\left(x_2^2-4\right)\)
\(=\left(x_1x_2\right)^2-4\left(x_1^2+x_2^2\right)+16\)
\(=\left(-8\right)^2-4\left[\left(x_1+x_2\right)^2-2x_1x_2\right]+16\)
\(=-4\left[\left(-m+2\right)^2-2\cdot\left(-8\right)\right]+80\)
\(=-4\left(m-2\right)^2-64+80\)
\(=-4\left(m-2\right)^2+16< =16\forall m\)
Dấu '=' xảy ra khi m=2








 không cần làm hết đâu ạ chỉ cần 2,3 câu là đc ạ
không cần làm hết đâu ạ chỉ cần 2,3 câu là đc ạ
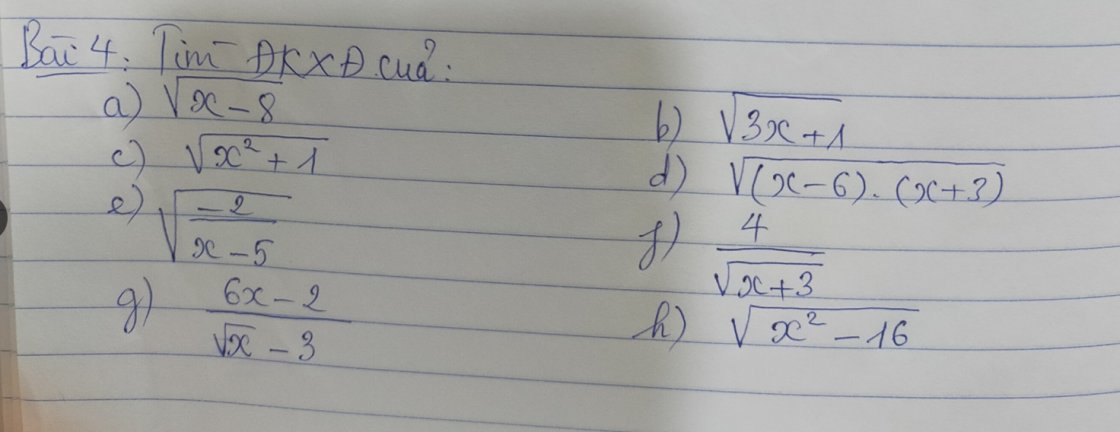



 không cần làm câu c đâu ạ, giúp e với nhaaa mn
không cần làm câu c đâu ạ, giúp e với nhaaa mn