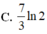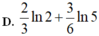Chọn D
Ta có: 1 x ( x + 3 ) = 1 3 1 x - 1 x + 3
Nên ∫ f ( x ) d x = ∫ 1 3 1 x - 1 x + 3 d x = 1 3 ln x x + 3 + C
Chọn D
Ta có: 1 x ( x + 3 ) = 1 3 1 x - 1 x + 3
Nên ∫ f ( x ) d x = ∫ 1 3 1 x - 1 x + 3 d x = 1 3 ln x x + 3 + C
Tính các nguyên hàm.
a)\(\int\dfrac{2dx}{x^2-5x}=A\ln\left|x\right|+B\ln\left|x-5\right|+C\) . Tìm 2A-3B.
b)\(\int\dfrac{x^3-1}{x+1}\)dx=\(Ax^3-Bx^2+x+E\ln\left|x+1\right|+C\).Tính A-B+E
Giải các bất phương trình sau:
a) (2x − 7)ln(x + 1) > 0;
b) (x − 5)(logx + 1) < 0;
c) 2 log 3 2 x + 5 log 2 2 x + log 2 x – 2 ≥ 0
d) ln(3 e x − 2) ≤ 2x
Tính các tích phân sau: 1) 2 ln e e x dx ; 2) 1 3 2 0 4 x dx x ; 3) /2 /4 1 tan dx x ; 4) 1 0 x e dx ; 5) 2 1 x xe dx ; 6) 0 1 3 4 dx x ; 7) 2 1 4 4 5 dx x x ; 8) 2 0 ln 1 x dx x (HD: 1 u x ) ĐS: 1) 2 e ; 2) 16 7 5 3 ; 3) ln 2 ; 4) 2
Biết ∫ 1 3 2 + ln ( x + 3 ) ( x + 1 ) 2 d x = a ln 2 + b ln 3 + c ( a , b , c ∈ ℚ ) . Giá trị 3a-b+2c bằng
A. 7
B. 0
C. -2
D. - 11 2
Cho hàm số f ( x ) = ln 2019 - ln x + 2 x tính tổng S = f ' ( 1 ) + f ' ( 3 ) + . . . + f ' ( 2019 )
A. 4305 2019
B. 2021
C. 2019 2021
D. 2020 2021
Biết I = ∫ 1 3 3 + ln x ( x + 1 ) 2 d x = a ( 1 + ln 3 ) - b ln 2 . Khi đó a 2 + b 2 bằng:
A. a 2 + b 2 = 7 16
B. a 2 + b 2 = 16 9
C. a 2 + b 2 = 25 16
D. a 2 + b 2 = 3 4
Bất phương trình ln(2x2 + 3) > ln(x2 + ax + 1) nghiệm đúng với mọi số thực x khi:
A. - 2 2 < a < 2 2
B. 0 < a < 2 2
C. 0 < a < 2
D. - 2 < a < 2
Cho hàm số y = f ( x ) liên tục trên 0 ; + ∞ .
Biết f ' ( x ) ln ( x ) x v à f ( 1 ) = 3 2 và tính f ( 3 )
![]()
![]()
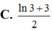
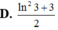
Tìm x để ba số ln2; ln( 2x - 1); ln( 2x + 3) theo thứ tự lập thành cấp số cộng.
A. 1
B. 2
C. log25
D. log23
Giả sử F(x) là một nguyên hàm của f ( x ) = ln ( x + 3 ) x 2 sao cho F(-2)+F(1)=0. Giá trị của F(-1)+F(2) bằng
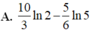
B. 0