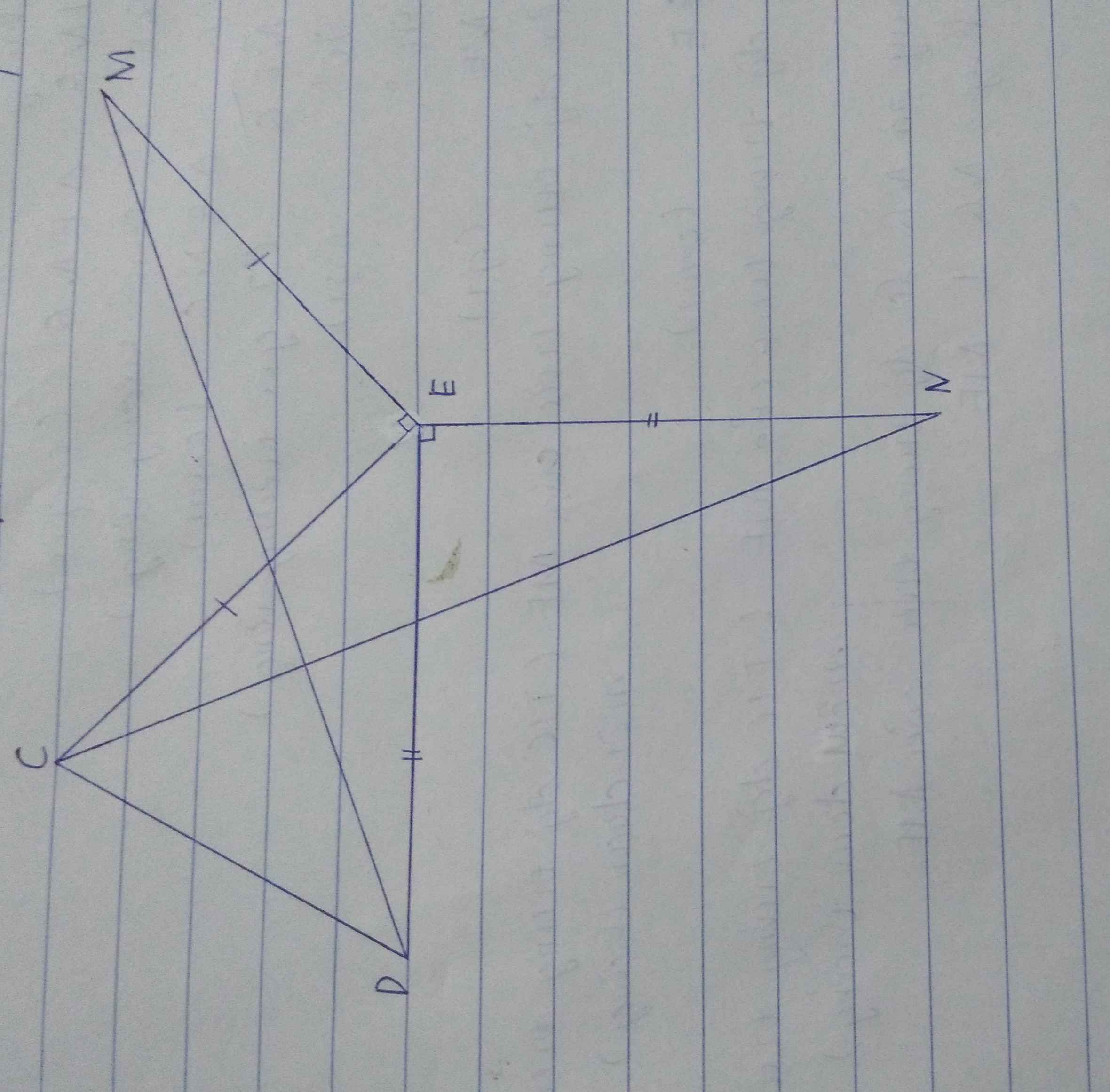
Bài 1:
a) Xét ΔMNQ và ΔENQ có
NM=NE(gt)
\(\widehat{MNQ}=\widehat{ENQ}\)(NQ là tia phân giác của \(\widehat{MNE}\))
NQ chung
Do đó: ΔMNQ=ΔENQ(c-g-c)
Suy ra: QM=QE(hai cạnh tương ứng)
b) Ta có: ΔMNQ=ΔENQ(cmt)
nên \(\widehat{NMQ}=\widehat{NEQ}\)(hai góc tương ứng)
mà \(\widehat{NMQ}=90^0\)(gt)
nên \(\widehat{NEQ}=90^0\)
c) Ta có: NM=NE(gt)
nên N nằm trên đường trung trực của ME(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: QM=QE(cmt)
nên Q nằm trên đường trung trực của ME(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra NQ là đường trung trực của ME
hay NQ\(\perp\)ME
Đúng 1
Bình luận (1)
