Question

Hình thang ABCD (AB//CD) có hai đường chéo cắt nhau tại O. Đường thẳng qua O và song son vớ đáy AB cắt các cạnh bên AD,BC theo thứ tự ở M và N.

a) Chứng minh : OA.BD=OB.AC

b) Chứng minh OM=ON

Answer 1

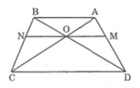
a: Xét ΔOAB và ΔOCD có

\(\widehat{OAB}=\widehat{OCD}\)(AB//CD)

\(\widehat{AOB}=\widehat{COD}\)(hai góc đối đỉnh)

Do đó: ΔOAB~ΔOCD

=>\(\dfrac{OA}{OC}=\dfrac{OB}{OD}\)

=>\(\dfrac{OC}{OA}=\dfrac{OD}{OB}\)

=>\(\dfrac{OC+OA}{OA}=\dfrac{OD+OB}{OB}\)

=>\(\dfrac{AC}{OA}=\dfrac{BD}{OB}\)

=>\(AC\cdot OB=AO\cdot BD\)

b: Xét ΔADC có OM//DC

nên \(\dfrac{OM}{DC}=\dfrac{AO}{AC}\left(1\right)\)

Xét ΔBDC có ON//DC

nên \(\dfrac{ON}{DC}=\dfrac{BO}{BD}\left(2\right)\)

Ta có: \(\dfrac{AC}{OA}=\dfrac{BD}{OB}\)

=>\(\dfrac{AO}{AC}=\dfrac{OB}{BD}\left(3\right)\)

Từ (3),(2),(1) suy ra OM=ON