Chọn đáp án D
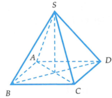
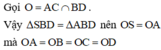
Suy ra, O cách đều tất cả các đỉnh của hình chóp.
Suy ra, O là tâm mặt cầu ngoại tiếp hình chóp S.ABCD.
Bán kính mặt cầu này
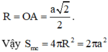
Chọn đáp án D

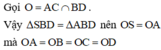
Suy ra, O cách đều tất cả các đỉnh của hình chóp.
Suy ra, O là tâm mặt cầu ngoại tiếp hình chóp S.ABCD.
Bán kính mặt cầu này
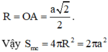
Hình chóp đều S.ABCD tất cả các cạnh bằng a. Diện tích mặt cầu ngoại tiếp hình chóp là:
A. 4 πa 2
B. πa 2
C. 2 πa 2
D. 2 πa 2
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng 2a. Thể tích khối cầu ngoại tiếp hình chóp là
A. 8 πa 3 2
B. 8 πa 3 2 3
C. 4 πa 3 2 3
D. πa 3 2 3
Diện tích mặt cầu ngoại tiếp hình chóp tứ giác đều có tất cả các cạnh bằng a
A. 2 πa 2 3
B. 2 πa 2
C. 4 πa 2 3
D. 4 πa 2
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng 2a. Tính bán kính R của mặt cầu ngoại tiếp hình chóp đã cho.
A. R = a 3 2
B. R = a 2 4
C. R = a 2
D. R = a 2 2
Hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mp(ABCD), S A = 2 a . Diện tích mặt cầu ngoại tiếp hình chóp S.ABCD bằng:
A. 2 π a 2
B. π a 2
C. 3 π a 2
D. 6 π a 2
Có ∫ 0 π 4 cos x sin x + cos x d x = π a + 1 b ln c với a , b , c ∈ ℤ thì a 2 + b + c là:
A. 14
B. 66
C. 66 + 2
D. 70
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a, các mặt bên tạo với đáy một góc 60 ∘ . Tính diện tích S của mặt cầu ngoại tiếp hình chóp.
A. S = 25 π a 2 3
B. S = 32 π a 2 3
C. S = 8 π a 2 3
D. S = a 2 12
Cho hình chóp S.ABCD đáy ABCD là hình chữ nhật cạnh AB = 2a,AD = a , ∆ S A D đều và nằm trong mặt phẳng vuông góc với đáy. Diện tích xung quanh của mặt cầu ngoại tiếp hình chóp S.ABCD là:
A. 16 π 3 a 2
B. 57 π 18 a 2
C. 48 π 9 a 2
D. 24 π 9 a 2
Cho hình chóp đều S.ABCD có cạnh đáy 2a và cạnh bên a 6 . Tính diện tích của mặt cầu ngoại tiếp hình chóp S.ABCD
A. 18 π a 2
B. 18 a 2
C. 9 a 2
D. 9 π a 2